
分析 先将x,y化简,在代入即可.
解答 解:∵x=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=5-2$\sqrt{6}$,
y=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$,
将x=5$-2\sqrt{6}$,y=5$+2\sqrt{6}$代入得,
原式=$\frac{2×\sqrt{10×10}-3×1}{3(49-20\sqrt{6})-5+3(49+20\sqrt{6})}$=$\frac{1}{17}$,
故答案为:$\frac{1}{17}$.
点评 本题主要考查了二次根式的化简求值,先将已知化简再代入是解答此题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
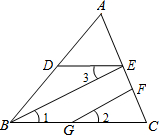 填写下题的步骤和依据.如图所示,已知△ABC中,FG∥BE,∠2=∠3,则∠EDB+∠DBC=180°?为什么?
填写下题的步骤和依据.如图所示,已知△ABC中,FG∥BE,∠2=∠3,则∠EDB+∠DBC=180°?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com