
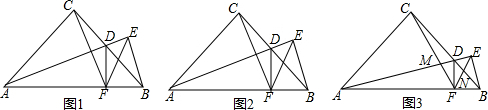
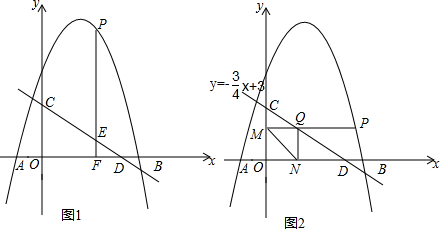
分析 (1)如图1,首先求出AD的长;可以判断△ACD∽△BED,列出关于BE的比例式,求出BE即可解决问题.
(2)如图2,运用角平分线的性质,结合正切函数的定义,首先求出tan∠DAC的值;然后证明∠CFD=∠EFD=∠DAC即可解决问题.
(3)如图3,作辅助线;首先证明PD=DQ;运用相似三角形的性质证明$\frac{DM}{MA}=\frac{DP}{AF}$,$\frac{DN}{NB}=\frac{DQ}{BF}=\frac{DQ}{DF}$,得到$\frac{DM}{MA}•\frac{NB}{DN}=\frac{DF}{AF}$,运用正切函数的定义即可解决问题.
解答 解:(1)如图1,∵△ABC为等腰直角三角形,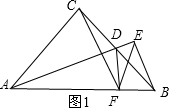
∴AC=BC,∠ACD=90°,而DC=DB=1,
∴AC=2,AD=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$;而BE⊥AE,
∴∠DEB=90°;而∠ACD=90°,∠ADC=∠BDE,
∴△ACD∽△BED,
∴$\frac{AC}{BE}=\frac{AD}{BD}$,
∴BE=$\frac{2\sqrt{5}}{5}$.
故答案为$\frac{2\sqrt{5}}{5}$
(2)如图2,设BC=AC=λ,则AB=$\sqrt{2}$λ;
∵∠CAD=∠BAD,
∴$\frac{AC}{AB}=\frac{CD}{BD}$,即$\frac{λ}{\sqrt{2}λ}=\frac{CD}{λ-CD}$,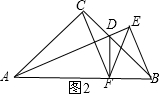
解得:CD=($\sqrt{2}-1$)λ,
∴tan∠DAC=$\frac{DC}{AC}$=$\sqrt{2}-1$;
∵DF⊥AB,∠ACD=90°,
∴∠ACD+∠AFD=180°,
∴A、C、D、F四点共圆,
∴∠CFD=∠DAC,同理可证∠EFD=∠DBE=∠DAF,
∴tan∠CFD=tan∠EFD=tan∠DAC=$\sqrt{2}-1$.
(3)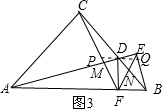 如图3,过点D作PQ∥AB,交CF于点P,交EF于点Q;
如图3,过点D作PQ∥AB,交CF于点P,交EF于点Q;
∵∠PFD=∠CAD,∠QFD=∠EBD,而∠CAD=∠EBD,
∴∠PFD=∠QFD,
∴tan∠PFD=tan∠QFD,
即$\frac{PD}{FD}=\frac{QD}{FD}$,
∴PD=QD;由∠DBF=45°,DF⊥BF知:
△BDF为等腰直角三角形,DF=BF;
∵DP∥AF,
∴△DPM∽△AFM,$\frac{DM}{MA}=\frac{DP}{AF}$;
同理可证:$\frac{DN}{NB}=\frac{DQ}{BF}=\frac{DQ}{DF}$,
∴$\frac{DM}{MA}•\frac{NB}{DN}=\frac{DF}{AF}$,而tan∠BAD=tan∠DAF=$\frac{DF}{AF}$,
∴tan∠BAD=$\frac{DM•NB}{DN•MA}$.
点评 该题以三角形为载体,以勾股定理、相似三角形的判定及其性质、四点共圆的判定及其性质、三角函数的定义等几何知识点为考查的核心构造而成;牢固掌握勾股定理、相似三角形的判定及其性质、四点共圆的判定及其性质等知识点是基础,灵活运用是关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
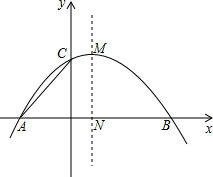 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
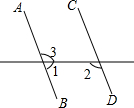 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )| A. | ∠2=70° | B. | ∠2=100° | C. | ∠2=110° | D. | ∠3=110° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com