
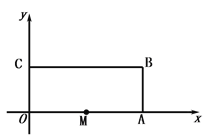
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ��8��0����C�������Ϊ��0��4������B�ڵ�һ�����ڣ���M��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-A-B-C-O��·���ƶ����˶���O��ֹͣ�˶�����
��1������M�ƶ���5��ʱ����M�������� ��
��2�����ƶ������У���M��y��ľ���Ϊ6����λ����ʱ�����M�ƶ���ʱ���� ��
��3�����ƶ������У���MB=MO�����M�ƶ���ʱ��.
���𰸡���1����8��2������2��3s��7s����3��![]() s��
s��![]() s.
s.
�������������������1����ʱ�估�ٶ������M�˶���·�߳������ݵ�M����O-A-B-C-O��·���ƶ����ɵó���M��λ����
��2���������������������M��OA�ϼ���M��CB��ͨ��ʱ�䣽·�����ٶȼ��ɵó��𰸣�
��3�������������M��OA�ϼ���M��CB�ϣ�Ȼ�����ù��ɶ����������.
�⣺��1����5��2��10����OA��8��
���M�˶���AB���ϣ��Ҿ��A��10-8��2����λ���ȣ�
���M�������ǣ�8��2��.
�ʴ�Ϊ����8��2��.
��2�������������
�ٵ�����OA��ʱ��M��6��0����
��M�˶�·��Ϊ6����λ���ȣ�
���˶�ʱ��Ϊ��6��2��3��s����
�ڵ�����BC��ʱ��M��6��4����
��M�˶�·��Ϊ8+4+2��14����λ���ȣ�
���˶�ʱ��Ϊ��14��2��7��s����
�ʴ�Ϊ��3s��7s.
��3�������������
�ٵ���M��OA��ʱ������BM��

��OM��a,��MB��a��AM��8-a,
��Rt��ABM�У��ɹ��ɶ����ã�
![]() ��
��
���� ![]()
��ã� ![]()
����OM��5��
���Ե�M�˶�ʱ��Ϊ�� ![]() ��s����
��s����
�ڵ���M��BC��ʱ������BO��

ͬ������BM��5��
���Ե�M�˶�ʱ��Ϊ�� ![]() ��s����
��s����
�ʴ�Ϊ�� ![]() s��
s��![]() s.
s.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
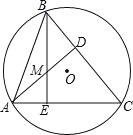
����Ŀ����ͼ����ABC�ڽ�����O��AD��BC��BE��AC��AD��BE�ཻ�ڵ�M����AC=8��BM=4������O�İ뾶���ڣ� ��
A��2![]() B��2
B��2![]() C��4
C��4![]() D��6
D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
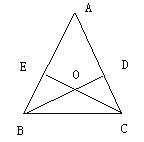
����Ŀ����֪����ͼ������ABC�У�AB=AC,BD��CE�Ǹ߲����ڵ�O.
��֤��(1)BD=CE����2��OB=OC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
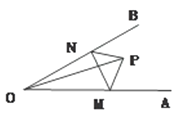
����Ŀ����ͼ����P�ǡ�AOB������һ�㣬OP=4cm����M�͵�N�ֱ�������OA������OB�ϵĶ��㣬��AOB=30������PMN�ܳ�����Сֵ=________ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ijˮ���۸���������ƣ�ij���е�һ����1000Ԫ����������ˮ���ܿ����꣬�ڶ�������960Ԫ������ˮ�������ڶ���ÿǧ�˵Ľ����ǵ�һ�ν��۵�1.2�������������ȵ�һ������20ǧ�ˣ�
��1�����һ�ι�������ˮ��ÿǧ�˵Ľ����Ƕ���Ԫ��
��2��������������Ӱ�죬�����г�����ˮ���������������٣��ó�����������������������������������������4a%��ÿǧ�˵Ľ����������ڵڶ��ν��۵Ļ���������5a%����������ڽ����ܶ�������ڽ����ܶ���16Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ���У��Գ��������ǣ� ��
A. ���������� B. �ȱ������� C. ������ D. Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������㣺������ʵ��a��b������a*b=a2��b�����磺3*2=32��2=7����ô2*����1��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��д�������
�٣���4��+����2��=�ڣ���4��������2��=�ۣ���4��������2��=�ܣ���4���£���2��=�ݣ���3��2=�ީ�3 2=
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com