
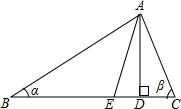
 如图在△ABC中,AD是BC边上的高线,AE是△ABC的角平分线,若∠B=α,∠C=β(α<β),用含α,β的代数式表示∠EAD.
如图在△ABC中,AD是BC边上的高线,AE是△ABC的角平分线,若∠B=α,∠C=β(α<β),用含α,β的代数式表示∠EAD. 分析 根据三角形的内角和定理求出∠BAC的度数,再根据角平分线的定义求出∠BAE的度数,根据直角三角形两锐角互余求出∠BAD的度数,然后根据∠DAE=∠BAD-∠BAE计算即可得解.
解答 解:∵∠B=α,∠C=β,
∴∠BAC=180°-α-β,
∵AD是△ABC的BC边上的高,
∴∠BAD=90°-α,
∵AE是∠BAC的角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-α-β),
∴∠DAE=∠BAD-∠BAE=90°-α-$\frac{1}{2}$(180°-α-β)
=90°-α-90°+$\frac{1}{2}$α+$\frac{1}{2}$β
=$\frac{1}{2}$(β-α).
点评 本题考查了三角形的角平分线,三角形的高线,以及三角形的内角和定理,仔细分析图形,观察出∠DAE=∠BAD-∠BAE,然后分别表示出∠BAD与∠BAE是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com