
【题目】某通讯器材商场,计划用40000元从厂家购进若干部新型手机,以满足市场需求. 已知该厂家生产三种不同型号的手机,出厂价分别为:甲种型号手机每部1200元,乙种型号手机每部400元,丙种型号手机每部800元.
(1)若该商场同时购进其中两种不同型号的手机共40部,并将40000元恰好用完. 请你帮助该商场研究一下进货方案;
(2)商场每销售一部甲种型号手机可获利120元,每销售一部乙种型号手机可获利80元,每销售一部丙种型号手机可获利120元,那么在同时购进两种不同型号手机的几种方案中,哪种进货方案获利最多?
【答案】(1) 共两种进货方案:方案1:甲种型号30部,乙种型号10部;方案2:甲种型号20部,丙种型号20部;(2) 购进甲种型号20部,丙种型号20部获利最多
【解析】
(1)本题的等量关系是,购进两种不同型号的手机的数量和=40部,购进两种手机的费用和=40000元.然后对分购进的是甲乙,甲丙,乙丙三种情况分别进行计算,然后得出进货方案;
(2)求出(1)中得出的两种方案的获利,比较得出获利最多的方案.
(1)设购进甲种型号x部,乙种型号y部,丙种型号z部,
方案1:购进甲、乙 ![]()
解得![]() ,
,
即甲种型号30部,乙种型号10部.
方案2:购进甲、丙 ![]()
解得![]() ,
,
即甲种型号20部,丙种型号20部.
方案3:购进乙、丙 ![]() ,
,
解得![]() 舍去,
舍去,
∴共两种进货方案:方案1:甲种型号30部,乙种型号10部;
方案2:甲种型号20部,丙种型号20部.
(2)方案1获利120×30+80×10=4400元;
方案2获利120×20+120×20=4800元,
∴第2种方案即购进甲种型号20部,丙种型号20部获利最多.
故答案为:(1) 共两种进货方案:方案1:甲种型号30部,乙种型号10部;方案2:甲种型号20部,丙种型号20部;(2) 购进甲种型号20部,丙种型号20部获利最多.


科目:初中数学 来源: 题型:
【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的点P,Q,给出如下定义:若点P到点Q的距离为d(d≥0),则称d为点P到点Q的d追随值,记作d[PQ].例如,在数轴上点P表示的数是2,点Q表示的数是5,则点P到点Q的d追随值为d[PQ]=3.
问题解决:
(1)点M,N都在数轴上,点M表示的数是1,且点N到点M的d追随值d[MN]=a(a≥0),则点N表示的数是_____(用含a的代数式表示);
(2)如图,点C表示的数是1,在数轴上有两个动点A,B都沿着正方向同时移动,其中A点的速度为每秒3个单位,B点的速度为每秒1个单位,点A从点C出发,点B表示的数是b,设运动时间为t(t>0).
①当b=4时,问t为何值时,点A到点B的d追随值d[AB]=2;
②若0<t≤3时,点A到点B的d追随值d[AB]≤6,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏在测量学校一幢教学楼AB的高度时,她先在点C测得教学楼的顶部A的仰角为30°,然后向教学楼前进12米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.
(结果精确到0.1米,参考数据: ![]() ≈1.73)
≈1.73)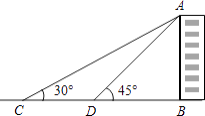
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF 
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com