
【题目】某商场试销一种成本为60元/件的夏季服装,规定试销期间销售单价不低于成本单价,且获利不得高于成本的50%,经市场试销调研发现,日销售量y(件)与售价x(元/件)符合一次函数y=kx+b,且当售价80元/件时,日销量为70件,当售价为70元件时,日销量为80件
(1)求一次函数y=kx+b的表达式;
(2)若该商场每天获得利润为w元,试写出利润w与售价x之间的关系式,并求出售价定为多少元时,商场每天可获得最大利润,最大利润是多少元?(利润=销售收入﹣进货成本,不含其他支出)
【答案】(1)y=﹣x+150;(2)当销售单价定为90元时,商场可获得最大利润,最大利润是1800元.
【解析】
(1)将“当售价80元/件时,日销量为70件,当售价为70元件时,日销量为80件”代入建立方程组,求出k和b的值,即可求出一次函数的表达式;
(2)先根据“![]() ”列出利润w的与售价x之间的关系式,再根据题意得出x的取值范围,利用二次函数的性质即可求解答案.
”列出利润w的与售价x之间的关系式,再根据题意得出x的取值范围,利用二次函数的性质即可求解答案.
(1)由题意得:![]()
解得:![]()
故所求一次函数的表达式为y=﹣x+150;
(2)由题意和题(1)的答案可得:
![]()
整理得:![]()
抛物线开口向下,当![]() 时,w随x的增大而增大
时,w随x的增大而增大
又因销售单价不低于成本单价,且获利不得高于50%
则![]() ,即
,即![]()
所以当![]() 时,w取得最大值为:
时,w取得最大值为:![]()
故当销售单价定为90元时,商场可获得最大利润,最大利润是1800元.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,且BD=CE,AD与BE相交于点F.
(1)求证:△ABD≌△BCE
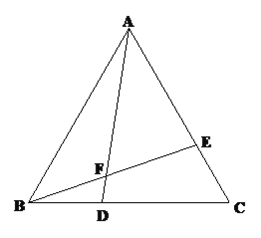
(2)求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE
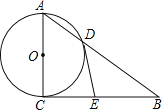
(1)求证:△DBE是等腰三角形
(2)求证:△COE∽△CAB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 今年的销售价格 | 2 |
那么新款B型节能电动车至少要购进多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
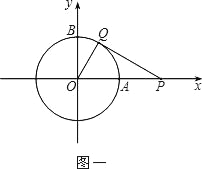
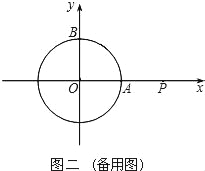
【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
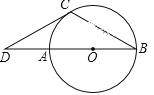
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
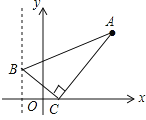
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com