
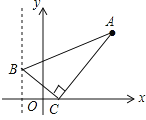
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
【答案】A
【解析】
设直线x=2与x轴交于G,过A作AH⊥直线x=2于H,AF⊥x轴于F,根据平行线的性质得到∠ABH=α,由三角函数的定义得到tanα=![]() ,即可得当BH最小时tanα有最大值;即BG最大时,tanα有最大值,然后证明△ACF∽△CBG,根据相似三角形的性质列出比例式,最后根据二次函数的性质即可得到结论.
,即可得当BH最小时tanα有最大值;即BG最大时,tanα有最大值,然后证明△ACF∽△CBG,根据相似三角形的性质列出比例式,最后根据二次函数的性质即可得到结论.
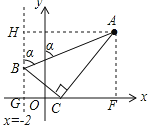
如图,设直线x=﹣2与x轴交于G,过A作AH⊥直线x=﹣2于H,AF⊥x轴于F,
∵BH∥y轴,
∴∠ABH=α,
在Rt△ABH中,tanα=![]() ,
,
∵tanα随BH的增大而减小,
∴当BH最小时tanα有最大值;即BG最大时,tanα有最大值,
∵∠BGC=∠ACB=∠AFC=90°,
∴∠GBC+∠BCG=∠BCG+∠ACF=90°,
∴∠GBC=∠ACF,
∴△ACF∽△CBG,
∴![]() ,
,
设BG=y,则![]() ,
,
∴![]() ,
,
∴当x=![]() 时,BG取最大值,tanα取最大值,
时,BG取最大值,tanα取最大值,
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为60元/件的夏季服装,规定试销期间销售单价不低于成本单价,且获利不得高于成本的50%,经市场试销调研发现,日销售量y(件)与售价x(元/件)符合一次函数y=kx+b,且当售价80元/件时,日销量为70件,当售价为70元件时,日销量为80件
(1)求一次函数y=kx+b的表达式;
(2)若该商场每天获得利润为w元,试写出利润w与售价x之间的关系式,并求出售价定为多少元时,商场每天可获得最大利润,最大利润是多少元?(利润=销售收入﹣进货成本,不含其他支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
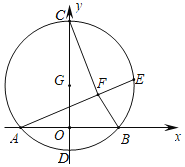
【题目】如图,以G(0,2)为圆心,半径为4的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为⊙G上一动点,且点E在第一象限,CF⊥AE于点F,当点E在⊙G的圆周上运动的过程中,线段BF的长度的最小值为( )
A.3B.2![]() 2C.6﹣2
2C.6﹣2![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D在⊙O上,连结BC,过D作PF∥AC交AB于E,交⊙O于F,交BC于点G,交过B点的直线于点P,且∠BPF=∠ADC.
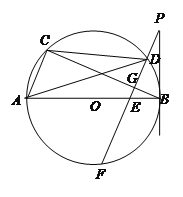
(1)判断直线BP与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为![]() ,AC=2,BE=1,求BP的长.
,AC=2,BE=1,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连结AE,交CD于点F
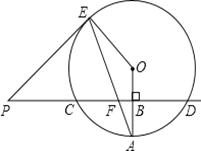
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
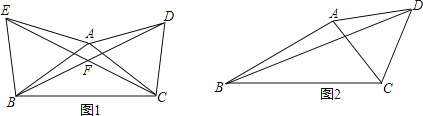
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为 ;
②若改变α、β的大小,且α+β=90°,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com