
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连结AE,交CD于点F
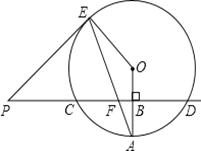
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=![]() ,求EF的长.
,求EF的长.
【答案】(1)CD=8![]() ;(2)证明见解析;(3)EF=10.
;(2)证明见解析;(3)EF=10.
【解析】
(1)首先连接OD,由直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,可求得OB的长,又由勾股定理,可求得BD的长,然后由垂径定理,求得CD的长.
(2)由PE是⊙O的切线,易证得∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF.
(3)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PFsinA=13×![]() =5,又由等腰三角形的性质,求得答案.
=5,又由等腰三角形的性质,求得答案.
解:(1)连接OD,
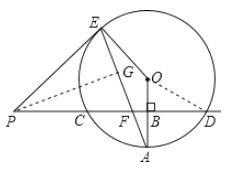
∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB=![]() OA=4,BC=BD=
OA=4,BC=BD=![]() CD.
CD.
∴在Rt△OBD中,![]() .
.
∴CD=2BD=8![]() .
.
(2)证明:
∵PE是⊙O的切线,
∴∠PEO=90°.
∴∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A.
∵OE=OA,
∴∠A=∠AEO.
∴∠PEF=∠PFE.
∴PE=PF.
(3)过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°.
∵∠PFG=∠AFB,
∴∠FPG=∠A.
∴FG=PFsinA=13×![]() =5.
=5.
∵PE=PF,∴EF=2FG=10.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
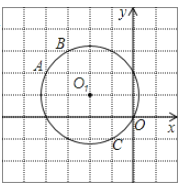
(1)在右边的平面直角坐标系中画出直线l,则直线l与⊙O1的交点坐标为 ;
(2)若⊙O1上存在点P,使得△APD为等腰三角形,则这样的点P有 个,试写出其中一个点P坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
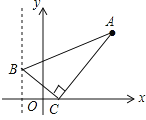
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
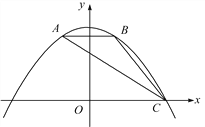
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,篮球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机,再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮正在参加学校举办的古诗词比赛节目,他须答对两道单选题才能顺利通过最后一关,其中第一题有A、B、C、D共4个选项,第二题有A、B、C共3个选项,而这两题小亮都不会,但小亮有一次使用“特权”的机会(使用“特权”可去掉其中一题的一个错误选项).
(1)如果小亮第一题不使用“特权”,随机选择一个选项,那么小亮答对第一题的概率是________.
(2)如果小亮将“特权”留在第二题,请用画树状图或列表法来求出小亮通过最后一关的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com