
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 恰好经过圆心
恰好经过圆心![]() ,连接
,连接![]() .
.
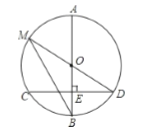
(1)若![]() ,
,![]() ,求
,求![]() 的直径;
的直径;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)20;(2)![]()
【解析】
(1)由CD=16,BE=4,根据垂径定理得出CE=DE=8,设⊙O的半径为r,则![]() ,根据勾股定理即可求得结果;
,根据勾股定理即可求得结果;
(2)由∠M=∠D,∠DOB=2∠D,结合直角三角形可以求得结果;
(2)由OM=OB得到∠B=∠M,根据三角形外角性质得∠DOB=∠B+∠M=2∠B,则2∠B+∠D=90°,加上∠B=∠D,所以2∠D+∠D=90°,然后解方程即可得∠D的度数;
解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设![]() ,
,
又∵BE=4,
∴![]()
∴![]() ,
,
解得:![]() ,
,
∴⊙O的直径是20.
(2)∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M=2∠B,
∵∠DOB+∠D=90°,
∴2∠B+∠D=90°,
∵![]() ,
,
∴∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°;


科目:初中数学 来源: 题型:
【题目】节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 今年的销售价格 | 2 |
那么新款B型节能电动车至少要购进多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
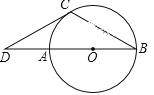
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
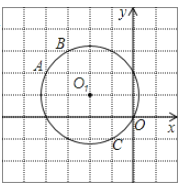
(1)在右边的平面直角坐标系中画出直线l,则直线l与⊙O1的交点坐标为 ;
(2)若⊙O1上存在点P,使得△APD为等腰三角形,则这样的点P有 个,试写出其中一个点P坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
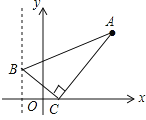
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,篮球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机,再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
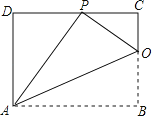
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com