
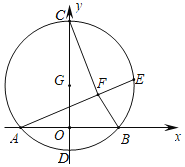
【题目】如图,以G(0,2)为圆心,半径为4的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为⊙G上一动点,且点E在第一象限,CF⊥AE于点F,当点E在⊙G的圆周上运动的过程中,线段BF的长度的最小值为( )
A.3B.2![]() 2C.6﹣2
2C.6﹣2![]() D.4
D.4![]()
【答案】C
【解析】
要求线段BF的最小值,首先要找到点F的运动轨迹,根据分析计算可知点F的运动轨迹是以AC为直径的圆,求出圆心与点B之间的距离,然后用该距离减去半径就是线段BF的最小值.
连接AC、BC,如图所示:
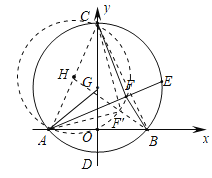
∵以G(0,2)为圆心,半径为4的圆与x轴交于A,B两点,与y轴交于C,D两点,
∴OC=6,OG=2,AG=4,OA=OB,AC=BC,
∴OA![]() 2
2![]() ,
,
AB=2OA=2×2![]() 4
4![]() ,
,
∵CF⊥AE,
∴∠CFA=90°,
在![]() 中,由勾股定理得
中,由勾股定理得
AC![]() 4
4![]() ,
,
∴点F的运动轨迹是以AC为直径的圆,设圆心为H,连接BH交⊙H于点F′,则BF′即为线段BF的最小长度,
∵AC=BC=AB=4![]() ,
,
∴△ABC是等边三角形,
∴△ABH是直角三角形,
AH![]() AC
AC![]() 4
4![]() 2
2![]() ,
,
BH![]() 6,
6,
∴BF′=BH﹣HF′=BH﹣AH=6﹣2![]() ,
,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE
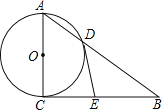
(1)求证:△DBE是等腰三角形
(2)求证:△COE∽△CAB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
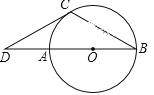
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
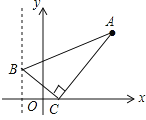
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
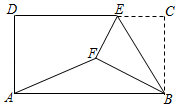
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com