
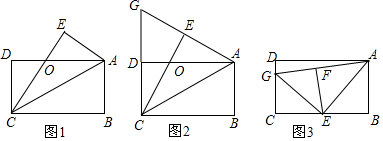
分析 先根据折叠的性质和矩形的性质证明△ADC≌△CEA,可得△OCA为等腰三角形;
(1)证明AG=CG,根据线段的和得出结论;
(2)如图3,根据折叠的性质得:BE=EF,∠B=∠EFA=90°,由HL证明Rt△ECG≌Rt△EFG,所以CG=GF,根据线段的和AG=AF+GF得出结论;
(3)如图4,作高线FH,根据特殊角的三角函数值和相似求DG、FH、GF、EF的长,代入面积公式计算即可.
解答 解:如图1,∵四边形ABCD为矩形,
∴CD=AB,BC=AD,∠CDA=∠B=90°,
由折叠得:BC=CE,AB=AE,∠B=∠CEA=90°,
∴CE=AD,AE=CD,∠CDA=∠CEA,
∴△ADC≌△CEA,
∴∠CAD=∠ECA,
∴OC=OA,
∴△OCA为等腰三角形;
(1)如图2,∵∠CDA=∠CEA=90°,∠DOC=∠EOA,
∴∠DCO=∠EAO,
∴∠DCO+∠OCA=∠EAO+∠OAC,
即∠DCA=∠CAG,
∴AG=CG,
∴AG-GD=CG-GD=CD,
∵AB=CD,
∴AB=AG-GD;
(2)如图3,AG=2AB-DG,理由是:
连接EG,
由折叠得:BE=EF,∠B=∠EFA=90°,
∴∠GFE=90°,
∵E是BC的中点,
∴EC=BE,
∴EC=EF,
∵∠C=90°,EG=EG,
∴Rt△ECG≌Rt△EFG(HL),
∴CG=GF,
∴AG=AF+GF=AB+CG,
∵CG=CD-DG=AB-DG,
∴AG=AB+AB-DG,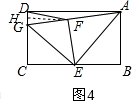
∴AG=2AB-DG;
(3)如图4,过F作FH⊥CD于H,
在Rt△AEB中,∵∠AEB=60°,∠B=90°,
∴tan60°=$\frac{AB}{BE}$,
∴BE=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
由(2)得:CE=EF=BE=$\sqrt{3}$,BC=2$\sqrt{3}$,
∵∠FEA=∠AEB=60°,
∴∠CEG=∠GEF=30°,
tan30°=$\frac{GF}{EF}$,
GF=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$=1,
∴CG=EF=1,
∴DG=2,
∵FH∥AD,
∴△GHF∽△GDA,
∴$\frac{FH}{AD}=\frac{GF}{AG}$,
∴$\frac{FH}{2\sqrt{3}}=\frac{1}{1+3}$,
FH=$\frac{\sqrt{3}}{2}$,
∴S四边形EFGD=S△DGF+S△GFE=$\frac{1}{2}$DG•FH+$\frac{1}{2}$FG•EF=$\frac{1}{2}$×$2×\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×$1×\sqrt{3}$=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题是四边形的综合题,考查了矩形的性质、等腰三角形的性质和判定、三角形相似或全等的性质和判定以及三角函数问题,第二问中三条线段的关系是以全等为突破口,利用线段的和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要6个这样的小立方块,最多需要8个这样的小立方块.
一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要6个这样的小立方块,最多需要8个这样的小立方块.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
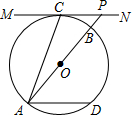 如图,已知A、C、D为⊙O上三点,过C的切线MN与弦AD平行,AD=2,AC=$\sqrt{5}$,延长AO交⊙O于B,交MN于P,则S△ACP=( )
如图,已知A、C、D为⊙O上三点,过C的切线MN与弦AD平行,AD=2,AC=$\sqrt{5}$,延长AO交⊙O于B,交MN于P,则S△ACP=( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{3}{2}\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com