
(8分)已知:如图,二次函数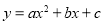 的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C (0,5),另抛物线经过点(1,8),M为它的顶点.
的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C (0,5),另抛物线经过点(1,8),M为它的顶点.
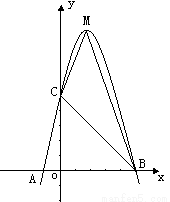
(1)求抛物线的解析式;
(2)求△MCB的面积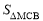 .
.
(1)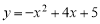 ;(2)15.
;(2)15.
【解析】
试题分析::(1)由A,C,D三点在抛物线上,代入函数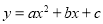 的解析式,构造方程组,解得抛物线的解析式;
的解析式,构造方程组,解得抛物线的解析式;
(2)过点M作平行与y轴的直线交BC于N,则△MCB的面积=△MCN的面积+△MNB的面积=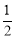 MNOB.
MNOB.
试题解析:(1)∵A(﹣1,0),C(0,5),D(1,8)在二次函数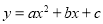 的图象上,
的图象上,
∴ ,解得:
,解得: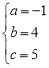 ,
,
∴抛物线的解析式为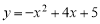 ;
;
(2)过点M作平行与y轴的直线交BC于N,
∵B点的坐标为:(5,0),∴BC的方程为: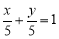 ,当x=2,y=3,故N点的坐标为(2,3),
,当x=2,y=3,故N点的坐标为(2,3),
函数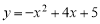 的顶点为(2,9),则MN=6,
的顶点为(2,9),则MN=6,
∴△MCB的面积=△MCN的面积+△MNB的面积=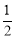 MNOB=15.
MNOB=15.
考点:1.二次函数的性质;2.函数的性质及应用.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:解答题
(8分)参加一次商品交易会的两家公司之间都签订了一份合同,所有公司共签订了45份合同,共有多少家公司参加商品交易会?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
A.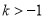 B.
B.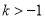 且
且  C.
C.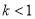 D.
D. 且
且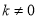
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
为解决群众看病难的问题,一种药品连续两次降价,每盒的价格由原来的60元降至48.6元,则平均每次降价的百分率为 _______ .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
关于x的一元二次方程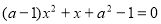 有一个根为0,则a的值是( )
有一个根为0,则a的值是( )
A、±1 B、-1 C、1 D、0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期中考试数学试卷(解析版) 题型:解答题
计算(每小题3分,共6分)
用适当的方法解下列方程(每小题4分,共8分)
(1)
(2)用配方法解方程:
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:计算题
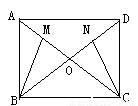
(6分)如图,矩形ABCD中,对角线AC和BD交于点O,M、N分别为OA、OD的中点。求证:BM=CN
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:填空题
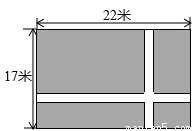
如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为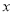 米,则根据题意可列出方程为 .
米,则根据题意可列出方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com