Question

【题目】已知函数f（x）= + （1﹣a2）x2﹣ax，其中a∈R．
（1）若曲线y=f（x）在点（1，f（1））处的切线方程为8x+y﹣2=0，求a的值；
（2）当a≠0时，求函数f（x）（x＞0）的单调区间与极值；
（3）若a=1，存在实数m，使得方程f（x）=m恰好有三个不同的解，求实数m的取值范围．

Answer 1

【答案】
（1）解：f'（x）=ax2+（1﹣a2）x﹣a，由8x+y﹣2=0可得f'（1）=﹣8，

即f'（1）=a+（1﹣a2）﹣a=﹣8，解得a=±3，

当a=3时，f（x）=x3﹣4x2﹣3x，f（1）=﹣6，f'（x）=3x2﹣8x﹣3，f'（1）=﹣8，

当a=﹣3时，f（x）=﹣x3﹣4x2+3，f（1）=﹣2，f'（x）=﹣3x2﹣8x+3，f'（1）=﹣8，

故曲线y=f（x）在点（1，f（1））处的切线方程为y+2=﹣8（x﹣1），即8x+y﹣6=0不符合题意，舍去，

故a的值为3

（2）解：当a≠0时，f′（x）=ax2+（1﹣a2）x﹣a=（x﹣a）（ax+1）=a（x﹣a）（x+ ），

当a＞0时，令f'（x）=0，则

当x变化时，f'（x），f（x）的变化情况如下表：

x	（﹣∞，﹣ ）	﹣	（﹣ ，a）	a	（a，+∞）
f'（x）	+	0	﹣	0	+
f（x）	↑	极大值	↓	极小值	↑

∴f（x）的单调递增区间为 ，单调递减区间为 ．

函数f（x）在 处取得最大值 ，且 ．

函数f（x）在x2=a处取得极小值f（a），且 ，

当a＜0时，令f'（x）=0，则 ，

当x变化时，f'（x），f（x）的变化情况如下表：

x	（﹣∞，a）	a	（a，﹣ ）	﹣	（﹣ ，+∞）
f'（x）	﹣	0	+	0	﹣
f（x）	↓	极小值	↑	极大值	↓

∴f（x）的单调递减区间为 ，单调递增区间为 ，

函数f（x）在 处取得极大值 ，

且 ．

函数f（x）在x2=a处取得极小值f（a），且

（3）解：若a=1，则 ，

由（2）可知 在区间（﹣∞，﹣1），（1，+∞）内增函数，在区间（﹣1，1）内为减函数，

函数f（x）在x1=1处取的极小值f（1），且 ．

函数f（x）在x2=﹣1处取得极大值f（﹣1），且 ．

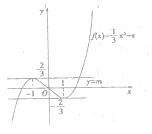
如图分别作出函数 与y=m的图象，

从图象上可以看出当 时，两个函数的图象有三个不同的交点，

即方程f（x）=m有三个不同的解，

故实数m的取值范围为 ．

【解析】（1）求导，由f'（1）=﹣8，求得a的值，分别求得切线方程，与原切线方程比较，即可求得a的值；（2）求导，根据导数与函数单调性的关系，分类讨论，即可求得函数f（x）（x＞0）的单调区间与极值；（3）由（2）可知：根据函数的单调性，求得f（x）的极值，分别作出函数 与y=m的图象，从图象上可以看出当 时，两个函数的图象有三个不同的交点，即可求得m的取值范围．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．