
【题目】如图1,△ABC中,CA=CB,∠ACB=120°,点E、F在AB上,且∠ECF=60°.
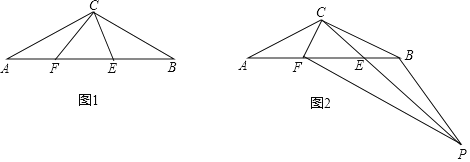
(1)①在图1中画出;点A关于直线CF的对称点G;②若EF=AF,求证:BE=EF;
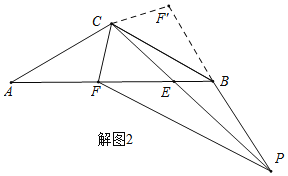
(2)如图2,∠ABP=120°,射线BP交CE的延长线于点P,求证:PB+AF=PF.
【答案】(1)①见解析,②见解析;(2)见解析.
【解析】
(1)根据对称的性质画出点G,根据对称的性质和全等三角形的性质可求证BE=EF.(2)将△ACF绕C点逆时针旋转至AC与BC重合,根据全等三角形的性质可求证PB+AF=PF.
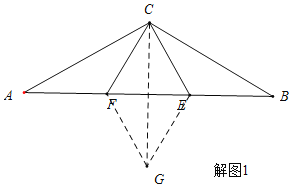
解:(1)①如解图(1):G为点A关于直线CF的对称点;
②连接FG、CG、EG,
∵G为点A关于直线CF的对称点;
∴△ACF≌△GCF,
∴AC=CG,∠ACF=∠GCF,∠FGC=∠A.
又∵AC=BC,
∴CG=CB,
∵∠ACB=120°,∠ECF=60°,
∴∠ECG=60°﹣∠GCF=60°﹣∠ACF,∠BCE=60°﹣∠ACF,
∴∠ECG=∠ECB,
在△GCE和△BCE中
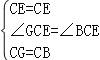
∴△GCE≌△BCE(SAS),
∴EG=BE,∠B=∠EGC,
∵∠ACB=120°,
∴∠A+∠B=60°,
∴∠EGC+∠FGC=60°,
又∵AF=EF=FG,
∴△FEG为等边三角形,
∴EF=EG=BE,即BE=EF.
(2)证明:由AC=BC,∠ACB=120°,故可将△ACF绕C点逆时针旋转120°到△BCF′位置,如解图2,
∵△ACF≌△BCF′,
∴∠A=∠CBA=∠CBF′=30°,AF=BF’,∠ACF=∠BCF′
又∵∠FBP=120°,
∴∠FBP+∠ABC+∠CBF′=180°,
∴B、P、F′在同一直线上,
又∵∠ACF+∠BCE=∠BCF′+∠BCE=60°,即∠PCF’=60°.
在△CFP和△CF′P中,
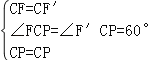 ,
,
∴△CFP≌△CF′P(SAS)
∴FP=F′P,
∵PB+BF′=BP+AF,
∴PB+AF=PF


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=![]() ;②0.5x=1;③
;②0.5x=1;③![]() =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程:
计算:(-15)÷![]() ×6.
×6.
解:原式=(-15)÷![]() ×6(第一步)
×6(第一步)
=(-15)÷(-1)(第二步)
=-15.(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第________步,错误的原因是________________;第二处是第________,错误的原因是________________.
(2)把正确的解题过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽查了10名同学的期末成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,-3,+12,-7,-10,-3,-8,+1,0,+10.
(1)这10名同学中最高分是多少?最低分是多少?
(2)10名同学中,低于80分的所占的百分比是多少?
(3)10名同学的总成绩是多少?平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
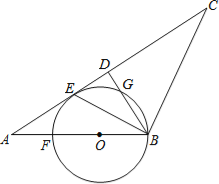
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1厘米的6个相同正方体摆成如图的形式.
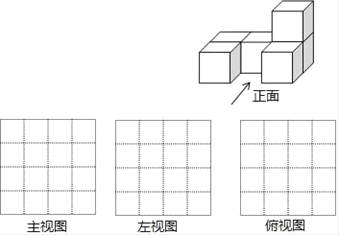
(1)画出该几何体的主视图、左视图、俯视图;
(2)直接写出该几何体的表面积为 cm2(包括底面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com