
【题目】如图,点B是线段AC上一点,AC=4AB,AB=6cm,直线MN经过线段BC的中点P.
(1)图中共有线段______条,图中共有射线______条.
(2)图中有______组对顶角,与∠MPC互补的角是______.
(3)线段AP的长度是______.

科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当OB绕点O在
当OB绕点O在![]() 内旋转时,则
内旋转时,则![]() 的大小为______;
的大小为______;
![]() 如图2,若
如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 当
当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小;
的大小;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 内绕着点O以
内绕着点O以![]() 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时,![]() 和
和![]() 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.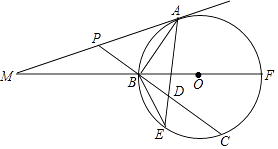
(1)求证: ![]() =
= ![]() ;
;
(2)若ED、EA的长是一元二次方程x2﹣5x+5=0的两根,求BE的长;
(3)若MA=6 ![]() ,sin∠AMF=
,sin∠AMF= ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= ![]() 交于E,F两点,若AB=2EF,则k的值是( )
交于E,F两点,若AB=2EF,则k的值是( )
A.﹣1
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com