
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.
【答案】
(1)证明:连接OD,
∵D是BC的中点,O为AB的中点,
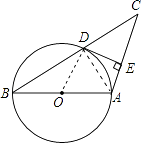
∴OD∥AC.
又∵DE⊥AC,
∴OD⊥DE,
∵OD为半径,
∴DE是圆O的切线.
(2)解:连接AD;
∵AB是圆O的直径,
∴∠ADB=90°=∠ADC,
∴△ADC是直角三角形.
∵∠C=30°,CD=10,
∴AD= ![]() .
.
∵OD∥AC,OD=OB,
∴∠B=30°,
∴△OAD是等边三角形,
∴OD=AD= ![]() ,
,
∴圆O的半径为 ![]() cm.
cm.
【解析】(1)连接OD,根据三角形的中位线定理可得OD∥AC.再根据平行线的性质就可证明DE是圆O的切线;(2)利用30°这个特殊角度,求出AD的长,由两直线平行同位角相等,可得∠B=30°,进而判断出△OAD是等边三角形,得到圆O的半径.
【考点精析】根据题目的已知条件,利用等边三角形的性质和圆周角定理的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点B是线段AC上一点,AC=4AB,AB=6cm,直线MN经过线段BC的中点P.
(1)图中共有线段______条,图中共有射线______条.
(2)图中有______组对顶角,与∠MPC互补的角是______.
(3)线段AP的长度是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
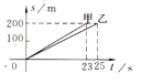
【题目】如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
(1)图象反映了哪两个变量之间的关系?
(2)他们进行的是多远的比赛?
(3)谁是冠军?
(4)乙在这次比赛中的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
![]()
(1)若AP=8 cm.
①运动1 s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)如果t=2 s时,CD=1 cm,试探索AP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com