
【题目】如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形边长为
(2)请用两种不同的方法表示图(2)阴影部分的面积;
方法一: 方法二:
(3)观察图(2),写出三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
(4)根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a﹣b)2的值.

【答案】(1)(m﹣n)m;(2)(m﹣n)2m2,[(m+n)2﹣4mn]m2;(3)(m﹣n)2=(m+n)2﹣4mn;(4)29
【解析】
(1)根据线段的和差关系即可求解;
(2)根据(1)中的结果即可得出答案;
(3)先根据(2)的结果进行变形,再代入求出即可;
(4)由(a-b)2=(a+b)2-4ab求解.
(1)图中阴影部分的正方形边长为(m﹣n)m.
故答案为:(m﹣n)m;
(2)方法一:∵图2中阴影部分为正方形边长为:(m﹣n)m
∴图2中阴影部分的面积是:(m﹣n)2m2
方法二:图2中阴影部分的面积=边长为(m+n)的正方形的面积﹣4个小长方形的面积和
即:[(m+n)2﹣4mn]m2
(3)关系为:(m﹣n)2=(m+n)2﹣4mn(4);
∵(m﹣n)2=(m+n)2﹣4mn;
∴有(a﹣b)2=(a+b)2﹣4ab
又∵a+b=7,ab=5
∴(a﹣b)2=(a+b)2﹣4ab=72﹣4×5=49﹣20=29.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
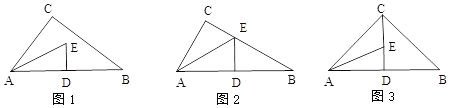
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )
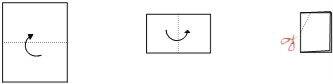
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, 在 ![]() 中,
中, ![]() ,
, ![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ![]() ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,正比例函数
中,正比例函数 ![]() 与反比例函数
与反比例函数 ![]() 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
(1)求反比例函数的表达式;
(2)若点P是反比例函数 ![]() 图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列因式分解的过程:
①x2-xy+4x-4y=(x2-xy)+(4x-4y)=x(x-y)+4(x-y)=(x-y)(x+4).
②a2-b2-c2+2bc=a2-(b2+c2-2bc)=a2-(b-c)2=(a+b-c)(a-b+c).
第①题分组后能直接提公因式,第②题分组后能直接运用公式,仿照上述分解因式的方法,把下列各式分解因式:
(1)ad-ac-bc+bd;
(2)x2-6x+9-y2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com