
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
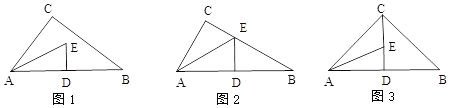
【答案】(1)①30°,②见解析;(2)见解析.
【解析】
(1)由∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E,可直接求出∠B的度数.先证明 BE=2DE,易得BC=3DE
(2) 过点E作EF⊥AC于点F,先证明△ABC是等腰直角三角形△CEF是等腰直角三角形,再证明△ADE≌△AFE(HL)即可.
(1)①∵AE平分∠CAB
∴∠CAE=∠DAE
又∵ED是AB的垂直平分线
∴EA=EB
∴∠B=∠DAE
∴∠CAE=∠DAE=∠B
又∵∠C=90°
∴∠B=![]() ×90°=30°
×90°=30°
②∵AE平分∠CAB,且EC⊥AC,ED⊥AB
∴EC=ED
在Rt△EDB中,∠B=30°
∴BE=2DE
BC=BE+CE=BE+DE=3DE
(2)过点E作EF⊥AC于点F,

∵ED是AB的垂直平分线,且C、E、D共线
∴CD也是AB的垂直平分线
∴CA=CB
又∠ACB=90°
∴△ABC是等腰直角三角形.
∴∠ACD=45°
∴△CEF是等腰直角三角形.
∴EF=CF
∵AE平分∠CAB,且EF⊥AC,ED⊥AB
∴EF=ED
∴ED=FC
在Rt△ADE和Rt△AFE中
EF=ED,AE=AE,
△ADE≌△AFE(HL)
∴AD=AF
∴BC=AC=AF+FC=AD+DE.


科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从下列![]() 、
、![]() 两题中任选一题作答,我选择: 题.
两题中任选一题作答,我选择: 题.
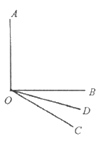
![]() :如图,已知
:如图,已知![]() ,射线
,射线![]() 在
在![]() 外部,且
外部,且![]() .若射线
.若射线![]() 平分
平分![]() .求
.求![]() 的度数.
的度数.
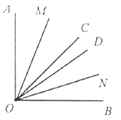
![]() :如图,已知
:如图,已知![]() ,射线
,射线![]() 在
在![]() 的内部,射线
的内部,射线![]() 在
在![]() 的内部,且
的内部,且![]() ,若射线
,若射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .求
.求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:
请利用直尺和圆规确定圆中弧AB所在圆的圆心![]()
小亮的作法如下:
如图:
① 在弧AB上任意取一点C,分别连接AC,BC
②分别作AC,BC的垂直平分线,两条垂线平分线交于O点,所以点O就是所求弧AB的圆心
老师说:“小亮的作法正确.”
请你回答:小亮的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.
(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形边长为
(2)请用两种不同的方法表示图(2)阴影部分的面积;
方法一: 方法二:
(3)观察图(2),写出三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
(4)根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a﹣b)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直径为 ![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0, ![]() ).
).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com