
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:
请利用直尺和圆规确定圆中弧AB所在圆的圆心![]()
小亮的作法如下:
如图:
① 在弧AB上任意取一点C,分别连接AC,BC
②分别作AC,BC的垂直平分线,两条垂线平分线交于O点,所以点O就是所求弧AB的圆心
老师说:“小亮的作法正确.”
请你回答:小亮的作图依据是 .
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
情境再现:
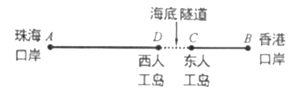
举世瞩目的港珠澳大桥东接香港,西接珠海、澳门,全长![]() 千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点
千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点![]() 至珠海口岸点
至珠海口岸点![]() 约
约![]() 千米,海底隧道
千米,海底隧道![]() 全长约
全长约![]() 千米,隧道一端的东人工岛点
千米,隧道一端的东人工岛点![]() 到香港口岸的路程为
到香港口岸的路程为![]() 千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.
千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.![]() 分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为
分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为![]() 千米/时,大客车的平均速度为
千米/时,大客车的平均速度为![]() 千米/时,私家车的平均速度为
千米/时,私家车的平均速度为![]() 千米/时.
千米/时.
问题解决:
(1)穿梭巴士出发多长时间与大客车相遇?
(2)私家车能否在到达珠海口岸前追上穿梭巴士?说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8 cm,BD=2 cm.
(1)图中共有多少条线段?
(2)求AC的长.
(3)若点E在直线AD上,且EA=3 cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
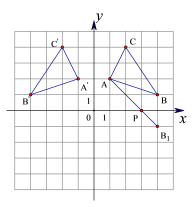
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).
(1)在图中画出△ABC关于y轴对称的图形△A’B’C’;
(2)在图中x轴上作出一点P,使PA+PB的值最小;并写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
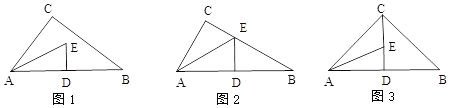
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )
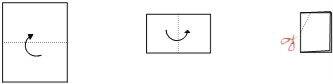
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,正比例函数
中,正比例函数 ![]() 与反比例函数
与反比例函数 ![]() 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
(1)求反比例函数的表达式;
(2)若点P是反比例函数 ![]() 图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com