
【题目】请从下列![]() 、
、![]() 两题中任选一题作答,我选择: 题.
两题中任选一题作答,我选择: 题.
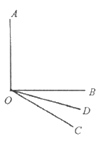
![]() :如图,已知
:如图,已知![]() ,射线
,射线![]() 在
在![]() 外部,且
外部,且![]() .若射线
.若射线![]() 平分
平分![]() .求
.求![]() 的度数.
的度数.
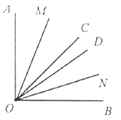
![]() :如图,已知
:如图,已知![]() ,射线
,射线![]() 在
在![]() 的内部,射线
的内部,射线![]() 在
在![]() 的内部,且
的内部,且![]() ,若射线
,若射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .求
.求![]() 的度数.
的度数.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.

被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
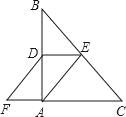
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
情境再现:
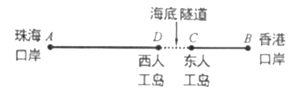
举世瞩目的港珠澳大桥东接香港,西接珠海、澳门,全长![]() 千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点
千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点![]() 至珠海口岸点
至珠海口岸点![]() 约
约![]() 千米,海底隧道
千米,海底隧道![]() 全长约
全长约![]() 千米,隧道一端的东人工岛点
千米,隧道一端的东人工岛点![]() 到香港口岸的路程为
到香港口岸的路程为![]() 千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.
千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.![]() 分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为
分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为![]() 千米/时,大客车的平均速度为
千米/时,大客车的平均速度为![]() 千米/时,私家车的平均速度为
千米/时,私家车的平均速度为![]() 千米/时.
千米/时.
问题解决:
(1)穿梭巴士出发多长时间与大客车相遇?
(2)私家车能否在到达珠海口岸前追上穿梭巴士?说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8 cm,BD=2 cm.
(1)图中共有多少条线段?
(2)求AC的长.
(3)若点E在直线AD上,且EA=3 cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
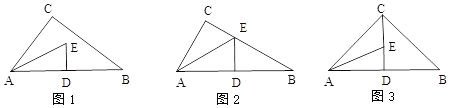
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com