
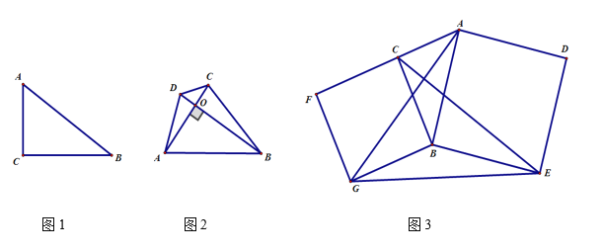
【题目】在直角三角形中,两直角边的平方和等于斜边的平方.如图1,若在△ABC中,∠C=90°,则AC2+BC2=AB2.我们定义为“商高定理”.
(1)如图1,在△ABC中,∠C=90°中,BC=4,AB=5,试求AC=__________;
(2)如图2,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;
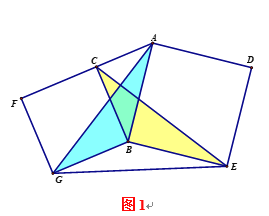
(3)如图3,分别以Rt△ACB的直角边BC和斜边AB为边向外作正方形BCFG和正方形ABED,连结CE、AG、GE.已知BC=4,AB=5,求GE2的值.
【答案】(1)AC=3; (2)见解析;(3)73.
【解析】
(1)根据勾股定理求出AC即可;
(2)在Rt△DOA中根据勾股定理有OD2+OA2=AD2,同理有OD2+OC2=CD2,OB2+OC2=BC2,OA2+OB2=AB2,又AB2+ CD2=OA2+OB2+ OD2+OC2,AD2+ BC2=OD2+OA2+ OB2+OC2
即可证明AB2+ CD2=AD2+ BC2;
(3)连接CG、AE,根据∠GBC=∠EBA=900得∠ABG=∠EBC,则证明△ABG≌△EBC,则∠1=∠2 ,∠3=∠4,由(2)可知AC2+GE2=CG2+AE2,则可求出CG2、AE2 、AC2从而求出GE2.
解:(1)在△ABC中,∠C=90°中,BC=4,AB=5
∴AC=![]() =3
=3
(2)在Rt△DOA中,∠DOA=900,
∴OD2+OA2=AD2
同理:OD2+OC2=CD2
OB2+OC2=BC2
OA2+OB2=AB2
∵AB2+ CD2=OA2+OB2+ OD2+OC2
AD2+ BC2=OD2+OA2+ OB2+OC2
∴AB2+ CD2=AD2+ BC2
(3)∵∠GBC=∠EBA=900
∴∠GBC+∠CBA=∠EBA+∠CBA
∴∠ABG=∠EBC
如图1,在△ABG和△EBC中
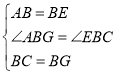
∴△ABG≌△EBC(SAS)
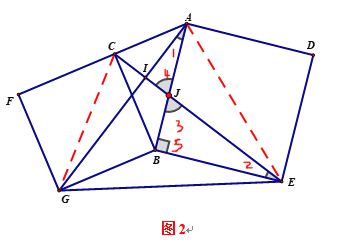
∴如图2,∠1=∠2 ,∠3=∠4
∴∠5=∠AIJ=900
∴AG⊥CB
连接CG、AE,
由(2)可知
AC2+GE2=CG2+AE2
在Rt△CBG中,CG2=BC2+BG2
CG2=42+42=32
在Rt△ABE中,AE2=BE2+AB2
AE2=52+52=50
在Rt△ABC中,AB2=AC2+BC2
52=AC2+42
AC2=9
∴AC2+GE2=CG2+AE2
9+ GE2=32+50
GE2=73


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
(1)求a的值;
(2)当0<t<2时,
①请探究∠ANM,∠OMN,∠BAN之间的数量关系,并说明理由;
②试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由。
(3)当OM=ON时,请求出t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】
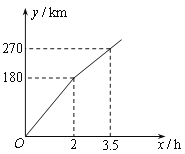
(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
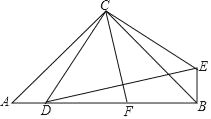
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组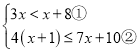 .请结合题意填空,完成本题的解答:
.请结合题意填空,完成本题的解答:
(1)解不等式①,得:________;
(2)解不等式②,得:________;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是( )

A. ②③ B. ②④ C. ②③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com