练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    小刚在研究矩形性质时，把两张完全相同的矩形纸片叠放在一起（如图中矩形ABCD和矩形BFDE），请你帮他判断重叠部分的四边形BNDM的性状，并给出证明．
    考点：菱形的判定
    专题：
    分析：首先根据矩形的性质可得MB∥DN，BN∥MD，进而得到四边形BNDM是平行四边形，再证明△ABM≌△EDM，可得BM=DM，然后根据邻边相等的平行四边形是菱形可得四边形BNDM是菱形．
    解答： 解：四边形BNDM是菱形，
    ∵四边形ABCD、BFDE是矩形，
    ∴MB∥DN，BN∥MD，
    ∴四边形BNDM是平行四边形，
    在△ABM和△EDM中，
    AB=DE
    ∠A=∠E=90°
    ∠AMB=∠EMD
    ，
    ∴△ABM≌△EDM（AAS），
    ∴BM=DM，
    ∴四边形BNDM是菱形．
    点评：此题主要考查了菱形的判定，关键是掌握邻边相等的平行四边形是菱形．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系xOy中，若动点P在抛物线y=ax2上，⊙P恒过点F（0，2），且与直线y=-2始终保持相切，则a=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

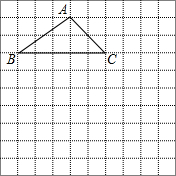    如图所示，在10×10正方形网格中，△ABC的三个顶点都在格点上，请按下列要求画图并回答问题：
    （1）画出将△ABC先向右平移3格，再向下平移5格后得到的△A1B1C1；
    （2）作△ABC的中线AD，△ACD的中线DE；
    （3）若△CDE的面积等于2，那么△A1B1C1的面积=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点，将直线y=-2x，沿y轴向上平移，分别交x轴，y轴于C、D两点．CD⊥CP，且CD=2CP，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

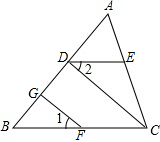    如图，在△ABC中，CD⊥AB于点D，FG⊥AB于点G，∠1=∠2，问DE与BC的关系如何，为什么？
    答：DE与BC
     

    理由如下：∵CD⊥AB，FG⊥AB（　　）
    ∴∠BGF=
     
    =90°（　　）
    ∴GF∥DC（　　）
    又∠BDC+∠DCB+∠B=180°（　　）
    ∠BGF+∠1+∠B=180°（　　）
    ∴∠1=
     
    （　　）
    又∠1=∠2（　　）
    ∴∠2=
     
    （　　）
    ∴
     
    ∥
     
    （　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    抛物线y=-
    1
    3
    x2可以看作是抛物线y=-
    1
    3
    （x-4）2向
     
    得到的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

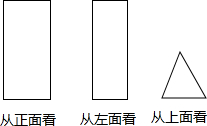    已知如图是三个方向看到的一个几何体的形状．
    （1）写出这个几何体的名称；
    （2）写出它的侧面展开的形状；
    （3）若从正面看到的高为10cm，从上面看到的三角形的三边长都为4cm，求这个几何体的侧面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知α是锐角且tanα=
    3
    4
    ，则sinα+cosα=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

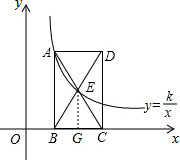    已知如图：点（1，3）在函数y=
    k
    x
    （x＞0）的图象上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=
    k
    x
    （x＞0）的图象又经过A、E两点，点E的横坐标为m，解答下列问题：
    （1）求k的值；
    （2）求点A的坐标；（用含m代数式表示）
    （3）当∠ABD=45°时，求m的值．

    查看答案和解析>>

    同步练习册答案