
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE. 
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD= ![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
【答案】
(1)解:连接BD、OD,如图,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E∵为斜边BC的中点,
∴CE=DE=BE= ![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线
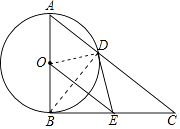
(2)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴BC:CD=AC:BC,
即BC2=ACCD.
∴BC2=2CDOE
(3)解:∵OE∥AC,
∴∠BOE=∠BAD,
在Rt△OBE中,cos∠BOE= ![]() =
= ![]() ,
,
设OB=3t,OE=5t,
则BE=4t,
∴4t=6,解得t= ![]() ,
,
∴OE=5t= ![]()
【解析】(1)利用圆周角定理得到∠ADB=90°,再利用直角三角形斜边上的中线性质得CE=DE=BE= ![]() BC,则∠C=∠CDE,加上∠A=∠ADO得到∠C+∠A=90°,然后证明∠ODE=90°,从而根据切线的判定方法可判定DE为⊙O的切线;(2)先证明OE是△ABC的中位线得到AC=2OE,再证明△ABC∽△BDC,则利用相似比和比例的性质可得到结论;(3)利用OE∥AC得到∠BOE=∠BAD,根据余弦定义得到cos∠BOE=
BC,则∠C=∠CDE,加上∠A=∠ADO得到∠C+∠A=90°,然后证明∠ODE=90°,从而根据切线的判定方法可判定DE为⊙O的切线;(2)先证明OE是△ABC的中位线得到AC=2OE,再证明△ABC∽△BDC,则利用相似比和比例的性质可得到结论;(3)利用OE∥AC得到∠BOE=∠BAD,根据余弦定义得到cos∠BOE= ![]() =
= ![]() ,则可设OB=3t,OE=5t,利用勾股定理得到BE=4t,于是得到4t=6,然后求出t后计算5t即可.
,则可设OB=3t,OE=5t,利用勾股定理得到BE=4t,于是得到4t=6,然后求出t后计算5t即可.


科目:初中数学 来源: 题型:
【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与C重合,折痕EF交AD于E,交BC于F,交AC于O,连结AF、CE. 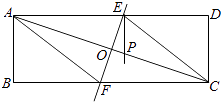
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:AE2=AOAP;
(3)若AE=8,△ABF的面积为9,求AB+BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,A、B、C是小正方形的顶点,求∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
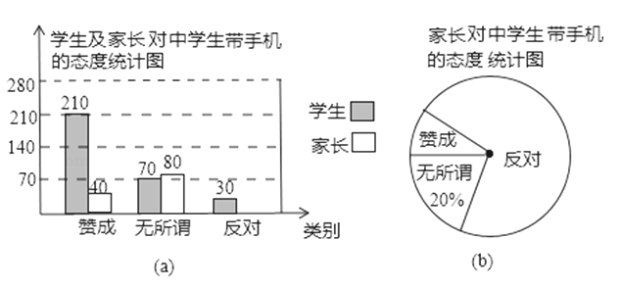
【题目】“校园手机”现象越来越受到社会的关注,记者张丽利用周末时间随机调查了某校若干名家长对中学生带手机现象的看法,统计整理并制作了如下的统计图,根据统计图信息完成下列问题:
(1)这次一共随机抽查了多少个学生家长进行调查;
(2)请将条形图补充完整;在扇形统计图中表示“赞成”的圆心角等于多少度;
(3)如果某校有3000名中学生家长,持“反对”态度的学生家长大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
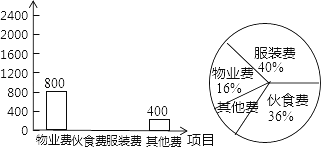
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com