
分析 (1)直接利用偶数的个数除以数字的总个数即可求得偶数的概率;
(2)列表或树状图将所有等可能的结果列举出来即可确定谁获胜的可能性大;
解答 解:(1)∵共有4个数字,有2个偶数,
∴P(偶数)=$\frac{2}{4}$=$\frac{1}{2}$;
(2)列表得:
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | (2,1) | (3,1) | (4,1) | |
| 2 | (1,2) | (3,2) | (4,2) | |
| 3 | (1,3) | (2,3) | (4,3) | |
| 4 | (1,4) | (2,4) | (3,4) |
点评 本题考查了列表法和树状图法,利用列表法或树状图法展示某一随机事件中所有等可能出现的结果数n,再找出其中某一事件所出现的可能数m,然后根据概率的定义可计算出这个事件的概率=$\frac{m}{n}$.


科目:初中数学 来源: 题型:解答题
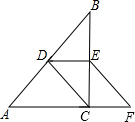 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
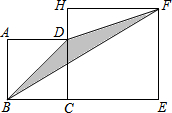 如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.
如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.
小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com