Question

11．连接四边形任意不相邻的两个顶点的线段叫做四边形的对角线，如图：

从四边形的一个顶点可以引出 1 条对角线，把四边形分成 2 个三角形；
从五边形的一个顶点可以引出 2 条对角线，把五边形分成 3 个三角形；
从六边形的一个顶点可以引出 3 条对角线，把六边形分成 4个三角形；
…
从n边形的一个顶点可以引出（n-3） 条对角线，把n边形分成（n-2）个三角形；
已知任意三角形的内角和为180°，则：
四边形的内角和为：180°×2
五边形的内角和为：180°×3
六边形的内角和为：180°×4
…
n边形的内角和为：（n-2）×180°（用含n的代数式表示）
根据上面你所找到的规律尝试计算十二边形的内角和，你一定能行．

Answer 1

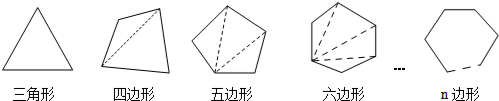
分析 根据三角形以及对角线的概念，不难发现：从一个顶点出发的对角线除了和2边不能组成三角形外，其余都能组成三角形．故过n边形的一个顶点的对角线可以把n边形分成（n-2）个三角形．从一个顶点出发画对角线除了相邻的两个顶点与自身外不能连接外，其余都能连接，故对角线有（n-3）条，根据多边形的内角和为（n-2）×180°解答即可．

解答 解：从n边形的一个顶点可以引（n-3）条对角线，并将n边形分成 （n-2）个三角形；
n边形的内角和为（n-2）×180°；
十二边形的内角和为（12-2）×180°=1800°．
故答案为：（n-3）；（n-2）；（n-2）×180°．

点评 本题考查了多边形的内角和定理的证明，解题关键是将多边形的内角和问题转化为三角形中解决，在n边形的任意一边上任取一点P，连接P点与其它各顶点的线段可以把n边形分成（n-2）个三角形．