
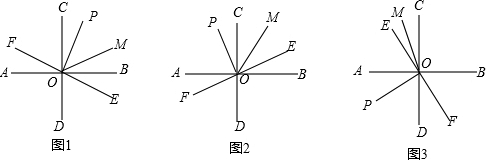
分析 (1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得$∠POM=\frac{1}{2}∠POB=\frac{1}{2}(90°-∠POC)$,∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,OP⊥OE,∠POM=90°-∠MOE,OM平分∠COE,∠COE=2∠MOE,由邻补角定义∠COF=180°-∠COE,等量代换得出结论;
(3)利用垂直的定义,OP⊥OE,∠POM=90°+∠MOE,OM平分∠COE,∠COE=2∠MOE,由邻补角定义∠COF=180°+∠COE,等量代换得出结论.
解答 解:(1)∠POM=$\frac{1}{2}$∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴$∠POM=∠MOB=\frac{1}{2}∠POB=\frac{1}{2}(90°-∠POC)$,
∵∠COF=90°-∠COP,
∴$∠POM=\frac{1}{2}∠COF$;
(2)不变化.
证明:∵OP⊥OE,
∴∠POM=90°-∠MOE,
∵∠COF=180°-∠COE,
∵OM平分∠COE,
∴∠COE=2∠MOE,
∴∠COF=180°-2∠MOE=2∠POM,
∴∠POM=$\frac{1}{2}$∠COF;
(3)不变化.
证明:∵OP⊥OE,
∴∠POE=90°,
∴∠POM=90°+∠EOM,
∠COF=180°+∠COE,
∵OM平分∠COE,
∴∠COE=2∠MOE,
∴∠COF=180°+2∠MOE,
∴∠POM=$\frac{1}{2}$∠COF;
点评 本题主要考查了垂直的定义,角平分线的性质,数形结合,找出角与角间的关系是解决此题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:解答题
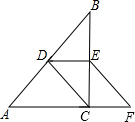 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
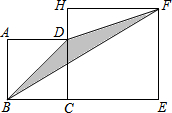 如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.
如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若∠A=30°,则l的最小值等于$\sqrt{3}$π | B. | 若∠A=45°,则l的最小值等于2π | ||
| C. | 若∠A=60°,则l的最小值等于$\frac{\sqrt{3}}{2}$π | D. | 若EF∥AB,则l等于2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.
小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
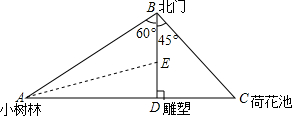 某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:
某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com