
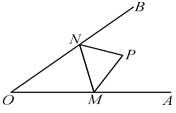
【题目】如图,![]() ,点
,点![]() 是
是![]() 内的一定点,点
内的一定点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上移动,当
上移动,当![]() 的周长最小时,
的周长最小时,![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
分别作点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,△PMN的周长最小值等于P1P2的长,然后依据等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2α,即可得出∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=180°﹣2α.
分别作点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O.
根据轴对称的性质可得MP=P1M,PN=P2N,∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB=2α,∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2α,∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2α.
故选B.



科目:初中数学 来源: 题型:
【题目】已知A(x,0),B(0,y),且x,y满足![]() ,且点A与点C关于y轴对称.
,且点A与点C关于y轴对称.
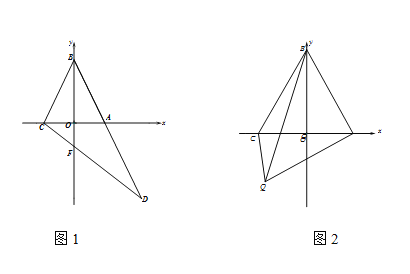
(1)求C坐标;
(2)如图1,点D在射线BA上,连接CD,若b=4,∠D=![]() ∠CBA,求CD长
∠CBA,求CD长
(3)如图2,如图2,BC=2OC,点Q是平面内一点,连接 QB,QC,QA,若QB=m,QC=OA,求AQ最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当ΔCB′E为直角三角形时,则AE的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,试判断四边形
,试判断四边形![]() 是什么样的四边形,并证明你的结论;
是什么样的四边形,并证明你的结论;
![]() 若
若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com