
(本题12分)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
(1) ;(2)当
;(2)当 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是 .
.
【解析】
试题分析:根据勾股定理求得AB=5cm.
(1)分类讨论:△AMP∽△ABC和△APM∽△ABC两种情况.利用相似三角形的对应边成比例来求t的值;
(2)如图,过点P作PH⊥BC于点H,构造平行线PH∥AC,由平行线分线段成比例求得以t表示的PH的值;然后根据“S=S△ABC﹣S△BPH”列出S与t的关系式S= (0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
(0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
试题解析:∵如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得 =5cm.
=5cm.
(1)以A,P,M为顶点的三角形与△ABC相似,分两种情况:①当△AMP∽△ABC时,
AP:AC=AM:AB,即 ,解得
,解得 ;
;
②当△APM∽△ABC时,AP:AB=AM:AC  =
= ,即
,即 ,
,
解得 (不合题意,舍去);
(不合题意,舍去);
综上所述,当 时,以A、P、M为顶点的三角形与△ABC相似;
时,以A、P、M为顶点的三角形与△ABC相似;
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:假设存在某一时刻t,使四边形APNC的面积S有最小值.
如图,过点P作PH⊥BC于点H.则PH∥AC,∴PH:AC=BP:BA,即PH:4=2t:5,∴PH= ,
,
∴S=S△ABC﹣S△BPN= =
= (0<t<2.5).
(0<t<2.5).
∵ ,∴S有最小值.当
,∴S有最小值.当 时,S最小值=
时,S最小值= .
.
答:当 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是 .
.

考点:相似形综合题.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:选择题
“如果二次函数 的图象与
的图象与 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程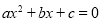 有两个不相等的实数根,”请根据你对这句话的理解,解决下面问题:若
有两个不相等的实数根,”请根据你对这句话的理解,解决下面问题:若 、
、 (
( )是关于
)是关于 的方程
的方程 的两根,且
的两根,且 ,则
,则 、
、 、
、 、
、 的大小关系是( )
的大小关系是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区八年级10月调研数学试卷(解析版) 题型:选择题
如图,ΔABC≌ΔADE,AB=AD,AC=AE,∠B=28º,∠E=95º,∠EAB=20º,则∠BAD为 ( )

A.75º B. 57º C. 55º D. 77º
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
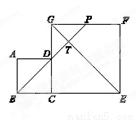
A.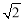 B.
B.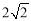 C.2 D.1
C.2 D.1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区八年级10月调研数学试卷(解析版) 题型:解答题
(8分)已知 ABC中∠BAC=150°,AB、AC的垂直平分线分别交BC于E、 F. 求∠EAF的度数.
ABC中∠BAC=150°,AB、AC的垂直平分线分别交BC于E、 F. 求∠EAF的度数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分)如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:填空题
在一个不透明的口袋中有3个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在15%左右,则口袋中的白球大约有_________个。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.


(1)求证:DE=EF;
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com