练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
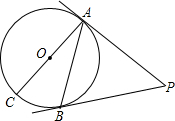
    17．如图，AC是⊙O的直径，PA，PB是⊙O的切线，A，B为切点，∠BAC=25°．求∠P的度数．

    分析 先根据切线长定理得到PA=PB，则利用等腰三角形的性质得∠PAB=∠PBA，再根据切线的性质得∠CAP=90°，于是利用互余计算出∠PAB=65°，然后根据三角形内角和定理计算∠P的度数．

    解答 解：∵PA，PB是⊙O的切线，
    ∴PA=PB，
    ∴∠PAB=∠PBA，
    ∵PA为切线，
    ∴CA⊥PA．
    ∴∠CAP=90°，
    ∵∠BAC=25°，
    ∴∠PAB=90°-∠BAC=65°，
    ∴∠P=180°-2∠PAB=50°．

    点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了切线长定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，点D在边BC上，AD=BD=AC，∠BAC=72°，则∠DAC=36°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

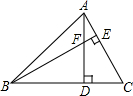    8．如图，△ABC中，∠ABC=45°，高AD、BE相交于点F，CD=4，则线段DF的长为（　　）
    A．2$\sqrt{2}$B．4C．3$\sqrt{2}$D．4$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知多项式x3-3xy2-4的常数项是a，次数是b．

    （1）则a=-4，b=3，并将这两数在数轴上所对应的点A，B表示出来；
    （2）数轴上在点B右边一点C到A，B两点的距离和为11，求点C在数轴上所对应的数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

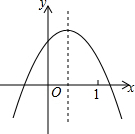    12．已知二次函数y=ax2+bx+c的图象如图所示，则下列选项中不正确的是（　　）
    A．a＜0B．c＞0C．0＜-$\frac{b}{2a}$＜1D．a+b+c＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．算式$（-\frac{1}{4}）×（-\frac{1}{4}）×（-\frac{1}{4}）×（-\frac{1}{4}）$可表示为（　　）
    A．$-\frac{{{1^{4}}}}{4}$B．$（-\frac{1}{4}）×4$C．${（-\frac{1}{4}）^4}$D．$-{（\frac{1}{4}）^4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．画出如图所示几何体的三视图．
    （1）主视图        
    （2）左视图         
    （3）俯视图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知点P（m，n）在第一象限，并且在一次函数y=2x-1的图象上，求实数m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）|$\sqrt{3}$-2|+$\root{3}{-8}$+（2-$\sqrt{3}$）×$\sqrt{3}$；
    （2）$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$．

    查看答案和解析>>

    同步练习册答案