
【题目】若等腰梯形两底角为30°,腰长为8,高和上底相等,则梯形中位线长为 ( )
A. 8![]() B. 10C. 4
B. 10C. 4![]() D. 16
D. 16![]()
【答案】C
【解析】
分析题意画出图形,则DE=CD=CF,AD=8,∠A=30°,由DE⊥AB,∠A=30°,AD=8,即可得出DE=4,进而求出CD的长度;运用勾股定理得出AE和BF的长度,易证四边形CDEF是平行四边形,得出EF的长度,进而得出AB+CD的长度,由梯形中位线的性质,即可解答本题.
根据题意画出图形,则DE=CD=CF,AD=8,∠A=30°.
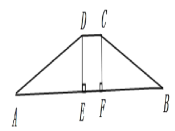
因为DE⊥AB,∠A=30°,AD=8,
所以DE=![]() AD=4,
AD=4,
所以CD=4,AE=![]() =4
=4![]() ,同理BF=4
,同理BF=4![]() .
.
因为DE⊥AB,CF⊥AB,
所以DE∥CF.
因为CD∥EF,
所以四边形CDEF是平行四边形,
所以EF=CD=4.
因为CD=4cm,AB=AE+EF+FB=4![]() +4+4
+4+4![]() =8
=8![]() +4,
+4,
所以AB+CD=8![]() +4+4=8
+4+4=8![]() +8,
+8,
所以梯形的中位线长为![]() (AB+CD)=4
(AB+CD)=4![]() +4.
+4.
故选C.


科目:初中数学 来源: 题型:
【题目】已知:直线![]() 经过点A(-5.-6)且与直线
经过点A(-5.-6)且与直线![]() : y=-
: y=-![]() x+6平行,直线
x+6平行,直线![]() 与x轴、y轴分别交于点B,C
与x轴、y轴分别交于点B,C
(1)求直线![]() 的表达式及其与x轴的交点D的坐标:
的表达式及其与x轴的交点D的坐标:
(2)判断四边形ABCD是什么四边形?并证明你的结论:
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标. 请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学2018年田径运动会上,参加跳高的运动员的成绩如表三所示.
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
(1)写出这些运动员跳高成绩的众数;
(2)该按2017年田径运动会上跳高的平均成绩为1.63m,则该校2018年田径运动会上跳高的平均成绩与2017年相比,是否有提高?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参数同学的成绩,整理并制作如下统计图:

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)补全频数分布直方图;
(3)在扇形统计图中,m= ,分数段60≤x<70的圆心角= °;
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在今年对全市![]() 名七年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.
名七年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.

请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() _______,
_______,![]() _______,
_______,![]() ________;
________;
(3)补全频数分布直方图;
(4)若视力在![]() 以上(含
以上(含![]() )均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?
)均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
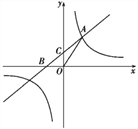
【题目】如图15,直线y=x+b与双曲线y=![]() 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com