Question

【题目】如图（1），菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点，四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上．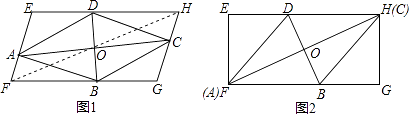

（1）求证：四边形EFGH是平行四边形；
（2）如图（2）若四边形EFGH是矩形，当AC与FH重合时，已知 =2，且菱形ABCD的面积是20，求矩形EFGH的长与宽．

Answer 1

【答案】
（1）证明：∵点O是菱形ABCD对角线AC、BD的交点，

∴OA=OC，OD=OB，

∵点O是线段FH的中点，

∴OF=OH．

在△AOF和△COH中，有 ，

∴△AOF≌△COH（SAS），

∴∠AFO=∠CHO，

∴AF∥CH．

同理可得：DH∥BF．

∴四边形EFGH是平行四边形

（2）设矩形EFGH的长为a、宽为b，则AC= ．

∵ =2，

∴BD= AC= ，OB= BD= ，OA= AC= ．

∵四边形ABCD为菱形，

∴AC⊥BD，

∴∠AOB=90°．

∵四边形EFGH是矩形，

∴∠AGH=90°，

∴∠AOB=∠AGH=90°，

又∵∠BAO=∠CAG，

∴△BAO∽△CAG，

∴ ，即 ，

解得：a=2b①．

∵S菱形ABCD= ACBD= =20，

∴a2+b2=80②．

联立①②得： ，

解得： ，或 （舍去）．

∴矩形EFGH的长为8，宽为4

【解析】（1）根据菱形的性质可得出OA=OC，OD=OB，再由中点的性质可得出OF=OH，结合对顶角相等即可利用全等三角形的判定定理（SAS）证出△AOF≌△COH，从而得出AF∥CH，同理可得出DH∥BF，依据平行四边形的判定定理即可证出结论；（2）设矩形EFGH的长为a、宽为b．根据勾股定理及边之间的关系可找出AC= ，BD= ，利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°，从而可证出△BAO∽△CAG，根据相似三角形的性质可得出 ，套入数据即可得出a=2b①，再根据菱形的面积公式得出a2+b2=80②，联立①②解方程组即可得出结论．本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质，解题的关键：（1）找出AF∥CH、DH∥BF；（2）找出关于a、b的二元二次方程组．本题属于中档题，难度不大，但解题过程叫繁琐，解决该题型题目时，根据相似三角形的性质找出对应边的比例关系是关键．