
����Ŀ����������������꼶�ϲ�α���������һ�仰�����ߺ�����һ�ߵĶԽǷֱ���ȵ����������β�һ��ȫ�ȡ�����������һ��̽��ʲô�����ȫ�ȣ�
������˼�������Dz�������������ת���ɷ������ԣ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
������̽����
��1����![]() ��
��![]() �����ʱ��
�����ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ���֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ���֤��������ȫ�ȣ���ٳ�������
��2����![]() ��
��![]() ��ֱ��ʱ��
��ֱ��ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ�ֱ��˵�����ɣ�����Ҫ֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ�ֱ��˵�����ɣ�����Ҫ֤��������ȫ�ȣ���ٳ�������
��3����![]() ��
��![]() �Ƕ۽�ʱ��
�Ƕ۽�ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ��������ͼ֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ��������ͼ֤��������ȫ�ȣ���ٳ�������
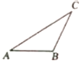
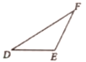
���𰸡���1��![]() ��
��![]() ��ȫ�ȣ���������������2��
��ȫ�ȣ���������������2��![]() ��
��![]() ȫ�ȣ����ɼ���������3��
ȫ�ȣ����ɼ���������3��![]() ��
��![]() ȫ�ȣ�֤��������
ȫ�ȣ�֤��������
��������
��1��������һ����������κ�һ���۽�����������![]() ���ɣ�
���ɣ�
��2����������ֱ��������ȫ�ȵ��ж�������![]() �������ɵã�
�������ɵã�
��3����ͼ�������������ȸ���������ȫ�ȵ��ж����������ʵó�![]() ���ٸ���ֱ��������ȫ�ȵ��ж����������ʵó�
���ٸ���ֱ��������ȫ�ȵ��ж����������ʵó�![]() ��Ȼ�����������ȫ�ȵ��ж��������ɵ�֤��
��Ȼ�����������ȫ�ȵ��ж��������ɵ�֤��
��1��![]() ��
��![]() ��ȫ��
��ȫ��
��������ͼ��ʾ��![]() ������Ȼ
������Ȼ![]() ��
��![]() ��ȫ�ȣ�
��ȫ�ȣ�
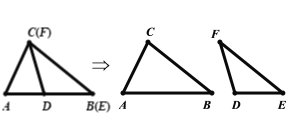
��2��![]() ��
��![]() ȫ��
ȫ��
���ɣ�б�ߺ�һ��ֱ�DZ߷ֱ���ȵ�����ֱ��������ȫ�ȣ���![]() ������
������
��3��![]() ��
��![]() ȫ�ȣ�֤�����£�
ȫ�ȣ�֤�����£�
��ͼ������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]()
��![]() ����
����![]() ��
��![]() ���Ƕ۽�
���Ƕ۽�
��![]() ����
����![]()
��![]() ��
��![]() ��
�У�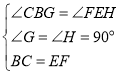
��![]()
��![]()
��![]() ��
��![]() ��
�У�![]()
��![]()
��![]()
��![]() ��
��![]() ��
�У�
��![]() ��
��
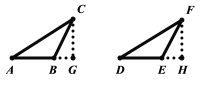



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У�BEƽ�֡�ABC��DE��BC.
(1)�Բ�����BDE����״����˵�����ɣ�
(2)����A��35������C��70�������BDE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
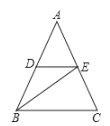
����Ŀ����һ���������У����һ��������һ���ǵ�3�������������������dz�֮Ϊ���鶯�����Ρ����磬�����ڽǷֱ�Ϊ120�㣬40�㣬20����������ǡ��鶯�����Ρ���
��ͼ����MON��60�㣬������OM����һ��A������A��AB��OM��ON�ڵ�B����AΪ�˵�������AD�����߶�OB�ڵ�C���涨0��< ��OAC < 90�㣩��
��1����ABO�Ķ���Ϊ�� ���㣬��AOB�� ������ǡ����ǡ��鶯�����Σ���
��2������BAC��60�㣬��֤����AOCΪ���鶯�����Ρ���
��3������ABCΪ���鶯�����Ρ�ʱ�����OAC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
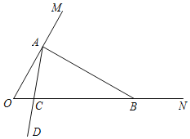
����Ŀ����ͼ����B��C�ֱ����߶�NM��NA�ϣ�����ABC�У���A�á�ABC�á�BCA��3��5��10������ABC�ա�MNC�����BCM�á�NBA����( )
A.1��2B.1��3C.1��4D.1��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��D��C��F��ͬһ��ֱ���ϣ�AD=CF��AB=DE��BC=EF.
(1)��֤����ABC����DEF��
(2)����A=55�㣬��B=88�������F�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�AE��CD��AD��BE�ཻ�ڵ�P��BQ��AD��Q��PQ��3��PE��1��AD�ij��ǣ�������
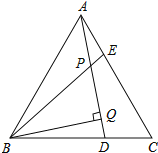
A.5B.6C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������C1��y=a1x2+b1x+c1��C2��y=a2x2+b2x+c2������ԭ�㣬����ֱ�ΪA��B����x�����һ������ֱ�ΪM��N�������A���B����M���N������ԭ��O�����ĶԳƣ���������C1��C2Ϊ���������ߣ�����д��һ�Խ���������C1��C2��ʹ�ı���ANBMǡ���Ǿ��Σ�����д��һ�������߽���ʽ��_______________________��_________________________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB=AC����ABΪֱ������O��BC�ڵ�D����AC�ڵ�E��
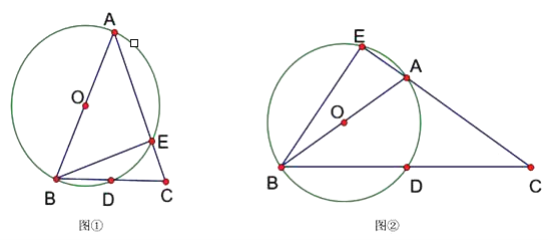
(1)����BACΪ���ʱ����ͼ������֤����CBE=![]() ��BAC��
��BAC��
(2)����BACΪ�۽�ʱ����ͼ�ڣ�CA���ӳ�������O�ཻ�ڵ�E��(1)�еĽ����Ƿ���Ȼ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��B�Ƿ���������y=��![]() ���ڵڶ������ڵķ�֧�ϵ������㣬��C��0��3�����ҡ�ABC����AC=BC����ACB=90�㣬���߶�AB�ij�Ϊ__��
���ڵڶ������ڵķ�֧�ϵ������㣬��C��0��3�����ҡ�ABC����AC=BC����ACB=90�㣬���߶�AB�ij�Ϊ__��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com