
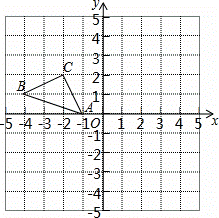
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出△ABC绕点A逆时针旋转90°的△AB2C2;
(3)点B1的坐标为__________,点C2的坐标为__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
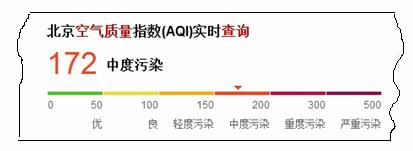
下图为北京某 天空气质量指数实时查询的一个结果.
天空气质量指数实时查询的一个结果.
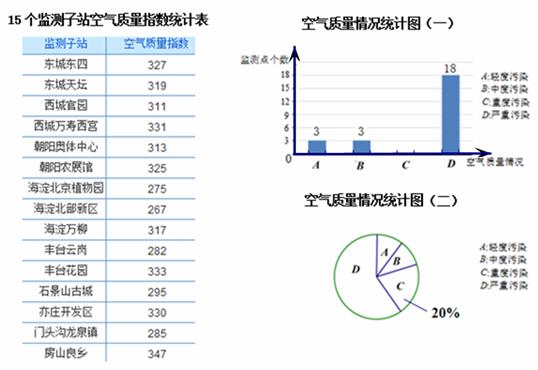
为了解今年北京市春节假期空气质量情况, 小静查到下表所示的某天15个监测子站的空气质量指数;小博从环境监测网随机抽取了某天部分监测点的空气质量情况,并绘制了以下两个统计图.
小静查到下表所示的某天15个监测子站的空气质量指数;小博从环境监测网随机抽取了某天部分监测点的空气质量情况,并绘制了以下两个统计图.
解答下列问题:
(1)小静查到的统计表中重度污染出现的频率为 ;(2)计算小博抽取的监测点的个数,并补全条形统计图;
(3)据统计数据显示,春节期间燃放烟花爆竹成为空气污染的一个重要原因. 市民在今年春节期间自觉减少了购买和燃放烟花爆竹的数量,全市销售烟花爆竹37万余箱,比去年减少35%.求今年比去年同期少销售多少万箱烟花爆竹.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
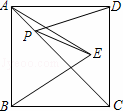
如图,正方形ABCD的面积为36cm2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是( )
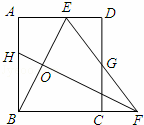
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在边长为6cm的正方形ABCD中,动点M、N从点A分别沿边A D、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.
D、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.
(1)试说明在运动过程中,四边形MNPQ是矩形;
(2)在运动过程中,当t为何值时,四边形MNPQ是正方形?
(3)在运动过程中,当t为何值时,△PNB沿折痕PN翻折得到△PNB′,使得 点B′恰好落在MQ上?
(4)将△MNA、△PNB、△PQC、△MQD同时沿折痕MN、PN、QP、MQ翻折,得△MNA′、△PNB′△PQC′、△MQD′,若其中两个三角形重叠部分的面积为4cm2,请直接写出动点运动时间t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
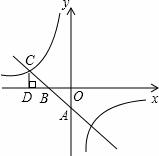
如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
(提示:先求出一次函数的解析式,得到点C的坐标,从而求出反比例函数解析式)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com