
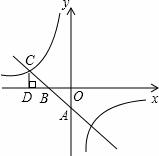
如图所示,一次函数与反比例函数的图象分别是直线AB和双曲线,直线AB与双曲线的一个交点为C,CD⊥x轴于点D,OD=2OB=4OA=4.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
(提示:先求出一次函数的解析式,得到点C的坐标,从而求出反比例函数解析式)
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
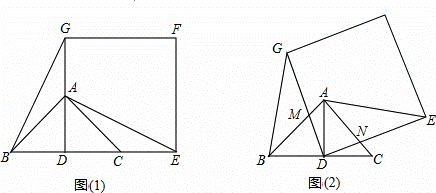
如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论:
(2)将正方形DEFG绕点D逆时针方向旋转一角度a后(0°<a<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由:
(3)若BC=DE=m,正方形DEFG绕点D逆时针方向旋转角度a(0°<a<360°)过程中,当AE为最大值时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
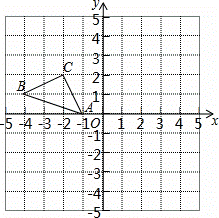
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出△ABC绕点A逆时针旋转90°的△AB2C2;
(3)点B1的坐标为__________,点C2的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线BF交AD于点E,交CD的延长线于点F,则DF=__________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
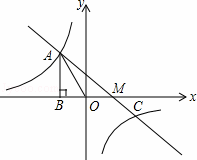
已知反比例函数 图象过第二象限内的点A(﹣2,m),作AB⊥x轴于点B,Rt△AOB面积为3.
图象过第二象限内的点A(﹣2,m),作AB⊥x轴于点B,Rt△AOB面积为3.
(1)求k和m的值;
(2)若直线y=ax+b经过点A,并且经过反比例函数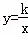
 的图象上另一点C(4,﹣
的图象上另一点C(4,﹣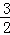 )
)
①求直线y=ax+b关系式;
②设直线y=ax+b与x轴交于M,求AM的长;
③根据图象写出使反比例函数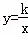 值大于一次函数y=ax+b的值的x的取值范围.
值大于一次函数y=ax+b的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
人民商场对上周女装的销售情况进行了统计,如下表所示:
 经理决定本周进女装时多进一些红色的,可用来解释这一现象的统计知识是( )
经理决定本周进女装时多进一些红色的,可用来解释这一现象的统计知识是( )
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示:
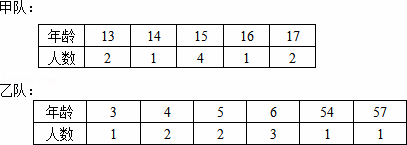
(1)根据上述数据完成下表:
 (2)根据前面的统计分析,回答下列问题:
(2)根据前面的统计分析,回答下列问题:
①能代表甲队游客一般年龄的统计量是__________;
②平均数能较好地反映乙队游客的年龄特征吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com