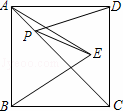
如图，正方形ABCD的面积为36cm2，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为__________．
53随堂测系列答案科目：初中数学 来源： 题型：
小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影
子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边
移动边观察，发现站到点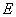
处时，可以使自己落在墙上的影子与这栋楼落在墙上的影
子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD＝1.2m，CE＝0.8m，
CA＝30m（点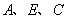
在同一直线上）．已知小明的身高
是1.7m，请你帮小明
求出楼高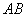
（结果精确到0.1m）．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图（1），已知△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点．作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG．
（1）试猜想线段BG和AE的关系（位置关系及数量关系），请直接写出你得到的结论：
（2）将正方形DEFG绕点D逆时针方向旋转一角度a后（0°＜a＜90°），如图（2），通过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由：
（3）若BC=DE=m，正方形DEFG绕点D逆时针方向旋转角度a（0°＜a＜360°）过程中，当AE为最大值时，求AF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
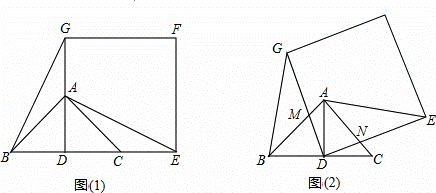
如图，两个边长均为2的正方形ABCD和正方形CDEF，点B、C、F在同一直线上，一直角三角板的直角顶点放置在D点处，DP交AB于点M，DQ交BF于点N．
（1）求证：△DBM≌△DFN；
（2）延长正方形的边CB和EF，分别与直角三角板的两边DP、DQ（或它们的延长线）交于点G和点H，试探究下列问题：
①线段BG与FH相等吗？说明理由；
②当线段FN的长是方程x2+2x﹣3=0的一根时，试求出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
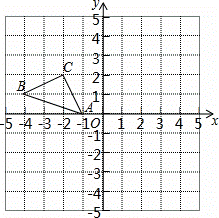
正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：
（1）作出△ABC关于原点O成中心对称的△A1B1C1；
（2）作出△ABC绕点A逆时针旋转90°的△AB2C2；
（3）点B1的坐标为__________，点C2的坐标为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
人民商场对上周女装的销售情况进行了统计，如下表所示：
经理决定本周进女装时多进一些红色的，可用来解释这一现象的统计知识是( )
A．平均数 B．中位数 C．众数 D．方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
）经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k=__________．
，
的最简公分母是__________．