
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘ”ăAŁš©3ŁŹ0Ł©ŁŹ¶țŽÎșŻÊęy=ax2+bx+ ![]() ”ĶԳÆÖáÎȘÖ±Ïßx=©1ŁŹÆäÍŒÏóčę”ăAÓëxÖ᜻ÓÚÁíÒ»”ăBŁŹÓëyÖ᜻ÓÚ”ăCŁź
”ĶԳÆÖáÎȘÖ±Ïßx=©1ŁŹÆäÍŒÏóčę”ăAÓëxÖ᜻ÓÚÁíÒ»”ăBŁŹÓëyÖ᜻ÓÚ”ăCŁź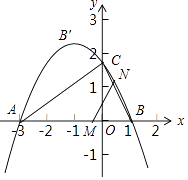
Łš1Ł©Çó¶țŽÎșŻÊę”ÄœâÎöÊœŁŹĐŽłö¶„”ăŚű±êŁ»
Łš2Ł©¶Ż”ăMŁŹNÍŹÊ±ŽÓB”ăłö·ąŁŹŸùÒÔĂżĂë2žöÈęλł€¶È”ÄËٶȷֱđŃŰĄśABC”ÄBAŁŹBC±ßÉÏÔ˶ŻŁŹÉèÆäÔ˶Ż”ÄʱŒäÎȘtĂ룏”±ÆäÖĐÒ»žö”ă”œŽïÖŐ”ăʱŁŹÁíÒ»žö”ăÒČËæ֟ͣÖčÔ˶ŻŁŹÁŹœáMNŁŹœ«ĄśBMNŃŰMN·ŐÛŁŹÈô”ăBÇĄșĂÂäÔÚĆŚÎïÏß»ĄÉÏ”ÄBĄäŽŠŁŹÊÔÇót”ÄÖ”Œ°”ăBĄä”ÄŚű±êŁ»
Łš3Ł©ÔÚŁš2Ł©”ÄÌőŒțÏÂŁŹQÎȘBN”ÄÖД㣏ÊÔÌœŸżŚű±êÖáÉÏÊÇ·ńŽæÔÚ”ăPŁŹÊč”ĂÒÔBŁŹQŁŹPÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜ABCÏàËÆŁżÈçčûŽæÔÚŁŹÇëÇółö”ăP”ÄŚű±êŁ»ÈçčûČ»ŽæÔÚŁŹÊÔ˔ÜÀíÓÉŁź
ĄŸŽđ°žĄż
Łš1Ł©
œâŁșÓÉÌâÒâ”Ă 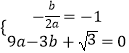 ŁŹ
ŁŹ
œâ”Ă 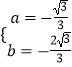 ŁŹ
ŁŹ
¶țŽÎșŻÊę”ÄœâÎöÊœÎȘy=© ![]() x2©
x2© ![]() x+
x+ ![]()
Ćä·œ”Ăy=© ![]() Łšx+1Ł©2+
Łšx+1Ł©2+ ![]() ŁŹ
ŁŹ
¶„”ăŚű±êÎȘŁš©1ŁŹ ![]() Ł©ŁŹ
Ł©ŁŹ
Łš2Ł©
œâŁșÈçÍŒ1
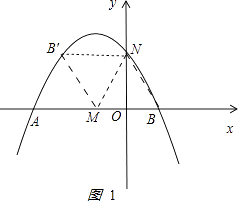 ŁŹ
ŁŹ
ÓÉÌâÒâÖȘOA=3ŁŹOB=1ŁŹON= ![]() ŁŹ
ŁŹ
ĄàĄÏCBA=60ĄăŁŹ
ÓÖĄßBM=BNŁŹ
ĄàĄśMBNÊÇŐęÈęœÇĐÎŁŹ
ĄàMŁš1©2tŁŹ0Ł©ŁŹNŁš1©tŁŹ ![]() tŁ©Łź
tŁ©Łź
œ«ĄśBMNŃŰMN·ŐÛșóŁŹ”Ă
BĄäN=BN=2tŁŹĄÏBĄäNM=ĄÏBMN=60ĄăŁŹ
ĄàBĄäNĄÎBMŁŹ
ĄàBĄäŁš1©3tŁŹ ![]() tŁ©ŁŹ
tŁ©ŁŹ
ÓÖ”ăBĄäÔÚĆŚÎïÏßÉÏŁŹ
Ąà ![]() t=©
t=© ![]() Łš1©3tŁ©2©
Łš1©3tŁ©2© ![]() Łš1©3tŁ©+
Łš1©3tŁ©+ ![]() ŁŹ
ŁŹ
»ŻŒòŁŹ”Ă9t2©9t=0ŁŹœâ”Ăt=0ŁšČ»·ûșÏÌâÒ⣏Éᣩt=1ŁŹ
t=1ʱŁŹ1©3t=©2ŁŹ ![]() t=
t= ![]() ŁŹ
ŁŹ
ĄàBĄäŁš©2ŁŹ ![]() Ł©Ł»
Ł©Ł»
Łš3Ł©
œâŁșÓÉÌâÒâżÉ”ĂĄśABCÊÇÖ±œÇÈęœÇĐÎŁŹÇÒĄÏBAC=30ĄăŁŹĄÏABC=60ĄăŁźÓÖQŁš ![]() ŁŹ
ŁŹ ![]() Ł©Łź
Ł©Łź
ąÙÈçÍŒ2
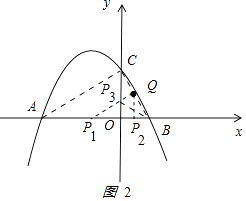 ŁŹ
ŁŹ
ÓÉÌâÒâÖȘOA=3ŁŹOB=1ŁŹ
PÔÚxÖáÉÏʱŁŹčęQŚśP1QĄÍBQœ»xÖáÓÚP1”㣏
ĄßP1QĄÎACŁŹ
Ąà1BQĄŚĄśABCŁŹ
![]() =
= ![]() =
= ![]() ŁŹ
ŁŹ
œâ”ĂP1B=2ŁŹOP1=1ŁŹP1Łš©1ŁŹ0Ł©Ł»
čęQŚśP2QĄÍxÖáÓÚP2ŁŹ
ĄßĄÏP2BQ=ĄÏCBAŁŹĄÏQPB=ĄÏACBŁŹ
ĄàQBP2ĄŚĄśABCŁŹ
![]() =
= ![]() ŁŹ
ŁŹ
œâ”ĂBP2= ![]() ŁŹOP2=
ŁŹOP2= ![]() ŁŹ
ŁŹ
P2Łš ![]() ŁŹ0Ł©Ł»
ŁŹ0Ł©Ł»
PÔÚxÖá”ÄÆäËüλÖĂʱŁŹĄśPBQČ»żÉÄÜÎȘÖ±œÇÈęœÇĐÎŁŹČ»żÉÄÜÓ륜ABCÏàËÆŁ»
ąÚÍŹÀíŁŹ”±PÔÚyÖáÉÏʱŁŹŚśP3QĄÍBQœ»yÖáÓÚP3ŁŹ
ĄßĄÏP3BQ=ĄÏBAC=ĄÏP3BO=30ĄăŁŹĄÏP3QB=ĄÏACB=90ĄăŁŹ
ĄàĄśBP3QĄŚĄśABCŁź
ĄßtanĄÏP3BO= ![]() =
= ![]() ŁŹP3O=
ŁŹP3O= ![]() ŁŹ
ŁŹ
P3Łš0ŁŹ ![]() Ł©Łź
Ł©Łź
BŚśP4BĄÍBQœ»yÓÚP4ŁŹ”« ![]() ĄÙ
ĄÙ ![]() ŁŹ
ŁŹ
ĄàĄśQBP4YÓ륜ABCČ»ÏàËÆŁŹPÔÚyÖáÉÏÆäËüλÖĂʱŁŹĄśPQBČ»ÎȘÖ±œÇÈęœÇĐÎŁŹČ»ÄÜÓ륜ABCÏàËÆŁ»
ŚÛÉÏËùÊöŁșŚű±êÖáÉÏŽæÔÚ”ăPŁŹÊč”ĂÒÔBŁŹQŁŹPÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜ABCÏàËÆŁŹP”ăŚű±êÎȘŁš©1ŁŹ0Ł©ŁŹŁš ![]() ŁŹ0Ł©ŁŹŁš0ŁŹ
ŁŹ0Ł©ŁŹŁš0ŁŹ ![]() Ł©Łź
Ł©Łź
ĄŸœâÎöĄżŁš1Ł©žùŸĘŽę¶šÏ”Êę·šŁŹżÉ”ĂșŻÊęœâÎöÊœŁŹžùŸĘĆä·œ·šŁŹżÉ”ö„”ăŚű±êŁ»Łš2Ł©žùŸĘ”ȱßÈęœÇĐΔÄĆжšŁŹżÉ”ĂĄśMBNÊÇŐęÈęœÇĐÎŁŹžùŸĘ·ŐÛ”ÄĐÔÖÊŁŹżÉ”ĂBĄäNŁŹĄÏBĄäNMŁŹžùŸĘÆœĐĐÏß”ÄĆжšŁŹżÉ”ĂBĄä”ÄŚĘŚű±êŁŹžùŸĘ”ă”ÄŚű±êÂúŚășŻÊęœâÎöÊœŁŹżÉ”ĂčŰÓÚt”Ä·œłÌŁŹžùŸĘœâ·œłÌŁŹżÉ”ĂtŁŹżÉ”ĂBĄä”ÄŚű±êŁ»Łš3Ł©žùŸĘÏàËÆÈęœÇĐΔÄĆжšÓëĐÔÖÊŁŹżÉ”Î𰞣ź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁËœâÄłÊĐÊĐĂńĄ°ÂÌÉ«łöĐĐĄ±·œÊœ”ÄÇéżöŁŹÄłĐŁÊęѧĐËÈ€ĐĄŚéÒÔÎÊŸí”śČé”ÄĐÎÊœŁŹËæ»ú”śČéÁËÄłÊĐČż·ÖłöĐĐÊĐĂń”ÄÖśÒȘłöĐĐ·œÊœŁšČÎÓëÎÊŸí”śČé”ÄÊĐĂń¶ŒÖ»ŽÓÒÔÏÂÎćžöÖÖÀàÖĐŃĄÔńÒ»ÀàŁ©ŁŹČąœ«”śČéœáčû»æÖÆłÉÈçÏÂČ»ÍêŐû”ÄÍłŒÆÍŒŁź
ÖÖÀà | A | B | C | D | E |
łöĐĐ·œÊœ | čČÏ프ł” | ČœĐĐ | č«œ»ł” | ”ÄÊż | ËœŒÒł” |

žùŸĘÒÔÉÏĐĆÏąŁŹ»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©ČÎÓ뱟ŽÎÎÊŸí”śČé”ÄÊĐĂńčČÓĐ ÈËŁŹÆäÖĐŃĄÔńBÀà”ÄÈËÊęÓĐ ÈËŁ»
Łš2Ł©ÔÚÉÈĐÎÍłŒÆÍŒÖĐŁŹÇóAÀà¶ÔÓŠÉÈĐÎÔČĐĜNJÁ”ĶÈÊ꣏ȹČčÈ«ÌőĐÎÍłŒÆÍŒŁ»
Łš3Ł©žĂÊĐÔŒÓĐ12ÍòÈËłöĐĐŁŹÈôœ«AŁŹBŁŹCŐâÈęÀàłöĐĐ·œÊœŸùÊÓÎȘĄ°ÂÌÉ«łöĐĐĄ±·œÊœŁŹÇëčÀŒÆžĂÊĐĄ°ÂÌÉ«łöĐĐĄ±·œÊœ”ÄÈËÊ꣟
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘĄśEFGĄŐĄśNMH, ĄÏFÓëĄÏMÊǶÔÓŠœÇŁź

Łš1Ł©ĐŽłöÏà”È”ÄÏ߶ÎÓëÏà”È”ÄœÇŁ»
Łš2Ł©ÈôEF=2.1cmŁŹFH=1.1cmŁŹHM=3.3cmŁŹÇóMNșÍHG”Äł€¶È.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘËıßĐÎABCDÖĐŁŹABĄÎDCŁŹÁŹœÓBDŁŹBEÆœ·ÖĄÏABDŁŹBEĄÍADŁŹĄÏEBCșÍĄÏDCB”ÄœÇÆœ·ÖÏßÏàœ»ÓÚ”ăFŁŹÈôĄÏADC=110ĄăŁŹÔòĄÏF”ĶÈÊęÎȘŁšĄĄĄĄŁ©
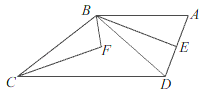
A. 115Ąă B. 110Ąă C. 105Ąă D. 100Ąă
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŁșčŰÓÚx”ÄÒ»ÔȘ¶țŽÎ·œłÌtx2©Łš3t+2Ł©x+2t+2=0ŁštŁŸ0Ł©
Łš1Ł©ÇóÖ€Łș·œłÌÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁ»
Łš2Ł©Éè·œłÌ”ÄÁœžöÊ”Êęžù·Ö±đÎȘx1 ŁŹ x2ŁšÆäÖĐx1ŁŒx2Ł©ŁŹÈôyÊÇčŰÓÚt”ÄșŻÊ꣏ÇÒy=x2©2x1 ŁŹ ÇóŐâžöșŻÊę”ÄœâÎöÊœŁŹČą»łöșŻÊęÍŒÏóŁ»
Łš3Ł©čÛČìŁš2Ł©ÖĐ”ÄșŻÊęÍŒÏóŁŹ”±yĄĘ2tʱŁŹĐŽłöŚÔ±äÁżt”ÄÈĄÖ”·¶Î§Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔĶÁČÄÁÏŁș ĐĄĂśÔÚŃ§Ï°¶țŽÎžùÊœșóŁŹ·ąÏÖÒ»Đ©șŹžùșĆ”ÄÊœŚÓżÉÒÔĐŽłÉÁíÒ»žöÊœŚÓ”ÄÆœ·œŁŹÈçŁș![]() ŁŹÉÆÓÚËŒżŒ”ÄĐĄĂśœűĐĐÁËÒÔÏÂÌœËśŁș
ŁŹÉÆÓÚËŒżŒ”ÄĐĄĂśœűĐĐÁËÒÔÏÂÌœËśŁș
Éè![]() ŁšÆäÖĐ
ŁšÆäÖĐ![]() ŸùÎȘŐûÊ꣩ŁŹÔòÓĐ
ŸùÎȘŐûÊ꣩ŁŹÔòÓĐ![]() Łź
Łź
Ąà![]() ŁźŐâŃùĐĄĂśŸÍŐÒ”œÁËÒ»ÖÖ°ŃČż·Ö
ŁźŐâŃùĐĄĂśŸÍŐÒ”œÁËÒ»ÖÖ°ŃČż·Ö![]() ”ÄÊœŚÓ»ŻÎȘÆœ·œÊœ”Ä·œ·šŁź
”ÄÊœŚÓ»ŻÎȘÆœ·œÊœ”Ä·œ·šŁź
ÇëÄă·ÂŐŐĐĄĂś”Ä·œ·šÌœËśČąœâŸöÏÂÁĐÎÊÌâŁș
”±![]() ŸùÎȘŐęŐûÊęʱŁŹÈô
ŸùÎȘŐęŐûÊęʱŁŹÈô![]() ŁŹÓĂșŹmĄąn”ÄÊœŚÓ·Ö±đ±íÊŸ
ŁŹÓĂșŹmĄąn”ÄÊœŚÓ·Ö±đ±íÊŸ![]() ŁŹ”Ă
ŁŹ”Ă![]() ŁœĄĄ ĄĄŁŹ
ŁœĄĄ ĄĄŁŹ![]() ŁœĄĄ ĄĄŁ»
ŁœĄĄ ĄĄŁ»
Łš2Ł©ÀûÓĂËùÌœËś”ÄœáÂÛŁŹŐÒÒ»ŚéŐęŐûÊę![]() ŁŹÌîżŐŁș Ł«ĄĄ ĄĄŁœ(ĄĄ ĄĄŁ«ĄĄ ĄĄ
ŁŹÌîżŐŁș Ł«ĄĄ ĄĄŁœ(ĄĄ ĄĄŁ«ĄĄ ĄĄ![]() )2Ł»
)2Ł»
Łš3Ł©Èô![]() ŁŹÇÒ
ŁŹÇÒ![]() ŸùÎȘŐęŐûÊ꣏Çó
ŸùÎȘŐęŐûÊ꣏Çó![]() ”ÄÖ”Łź
”ÄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒŁŹ”ăAŁŹBŁŹCÈę”ăÔÚĄŃOÉÏŁŹAEÆœ·ÖĄÏBACŁŹœ»ĄŃOÓÚ”ăEŁŹœ»BCÓÚ”ăDŁŹčę”ăEŚśÖ±ÏßlĄÎBCŁŹÁŹœáBEŁź 
Łš1Ł©ÇóÖ€ŁșÖ±ÏßlÊÇĄŃO”ÄÇĐÏߣ»
Łš2Ł©ÈçčûDE=aŁŹAE=bŁŹĐŽłöÇóBE”Äł€”Äˌ·Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘčŰÓÚx”Ä·œłÌx2+2x+a©2=0Łź
Łš1Ł©ÈôžĂ·œłÌÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁŹÇóÊ”Êęa”ÄÈĄÖ”·¶Î§Ł»
Łš2Ł©”±žĂ·œłÌ”ÄÒ»žöžùÎȘ1ʱŁŹÇóa”ÄÖ”Œ°·œłÌ”ÄÁíÒ»žùŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżčŰÓÚžĆÂÊŁŹÏÂÁĐË”·šŐęÈ·”ÄÊÇŁš Ł©
A.ÜìÏŰĄ°ĂśÌ윔Óê”ÄžĆÂÊÊÇ75%Ą±±íÜÜÌìÜìÏŰ»áÓĐ75%”ÄʱŒä»áÏÂÓê
B.Ëæ»úĆŚÖÀÒ»Ă¶ÖÊ”ŰŸùÔÈ”ÄÓČ±ÒŁŹÂä”ŰșóÒ»¶š·ŽĂæÏòÉÏ
C.ÔÚÒ»ŽÎłéœ±»î¶ŻÖĐŁŹÖĐœ±”ÄžĆÂÊÊÇ1%ŁŹÔòłéœ±100ŽÎŸÍÒ»¶š»áÖĐœ±
D.ÍŹÊ±ĆŚÖÀÁœĂ¶ÖÊ”ŰŸùÔÈÓČ±ÒŁŹĄ°Ò»Ă¶ÓȱÒŐęĂæÏòÉÏŁŹÒ»Ă¶ÓČ±Ò·ŽĂæÏòÉÏĄ±”ÄžĆÂÊÊÇ ![]()
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com