
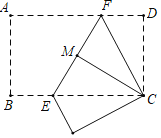
【题目】如图,把一张矩形纸片折叠,点A与点C重合,折痕为EF,再将△CDF沿CF折叠,点D恰好落在EF上的点M处,若BC=6厘米,则EF的长为_____厘米.
【答案】4
【解析】
由矩形的性质可得AD=BC=6cm,∠D=90°,AD∥BC,由折叠的性质可得CD=CM,∠D=∠FMC=60°,FD=FM,∠DFC=∠MFC,AF=CF,∠AFE=∠EFC,由平角的定义可得AFE=∠EFC=∠DFC=60°,可证△EFC是等边三角形,可求解.
解:∵四边形ABCD是矩形
∴AD=BC=6cm,∠D=90°,AD∥BC
∵把一张矩形纸片折叠,点A与点C重合,
∴AF=CF,∠AFE=∠EFC
∵将△CDF沿CF折叠,点D恰好落在EF上的点M处,
∴CD=CM,∠D=∠FMC=60°,FD=FM,∠DFC=∠MFC
∴∠AFE=∠EFC=∠DFC,且∠AFE+∠EFC+∠DFC=180°
∴∠AFE=∠EFC=∠DFC=60°,
∴∠FCD=30°
∴FC=2FD,
∴AF=2FD,
∵AD= BC=6厘米,
∴FD=2厘米,AF=4厘米=FC,
∵AD//BC
∴∠AFE=∠FEC=60°,且∠EFC=60°
∴△EFC是等边三角形
∴EF=FC=4厘米
故答案为:4


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m,坝高为6m,则坝底AB的长为_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
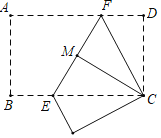
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴正半轴上),
轴正半轴上),![]() 为等腰直角三角形,且面积为
为等腰直角三角形,且面积为![]() ,现将抛物线沿
,现将抛物线沿![]() 方向平移,平移后的抛物线过点
方向平移,平移后的抛物线过点![]() 时,与
时,与![]() 轴的另一点为
轴的另一点为![]() ,其顶点为
,其顶点为![]() ,对称轴与
,对称轴与![]() 轴的交点为
轴的交点为![]() .
.
![]() 求
求![]() 、
、![]() 的值.
的值.
![]() 连接
连接![]() ,试判断
,试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
![]() 现将一足够大的三角板的直角顶点
现将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=![]() +1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)函数y=![]() +1的自变量x的取值范围是 ;
+1的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x | … | ﹣ | ﹣1 | ﹣ | 0 |
|
| 2 |
| 3 |
| … |
y | … |
| m |
| 0 | ﹣1 | n | 2 |
|
|
| … |
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.

(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
②当函数值![]() +1>
+1>![]() 时,x的取值范围是:
时,x的取值范围是:
③方程![]() +1=x的解为:
+1=x的解为:
查看答案和解析>>
科目:初中数学 来源: 题型:
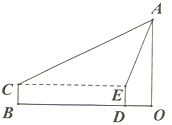
【题目】某中学为数学实验“先行示范校”,一数学活动小组带上高度为1.5m的测角仪BC,对建筑物AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进40m至DE处,测得顶点A的仰角为75°.
(1)求∠CAE的度数;
(2)求AE的长(结果保留根号);
(3)求建筑物AO的高度(精确到个位,参考数据:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是矩形
是矩形![]() 内的任意一点,连接
内的任意一点,连接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() ,
,![]() , 给出如下结论:①
, 给出如下结论:①![]() ②
②![]() ③若
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]() 点在矩形的对角线上.其中正确的结论的序号是( )
点在矩形的对角线上.其中正确的结论的序号是( )

A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
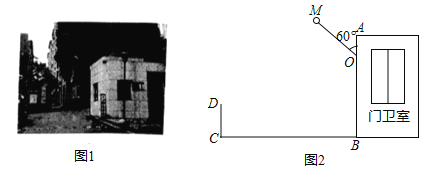
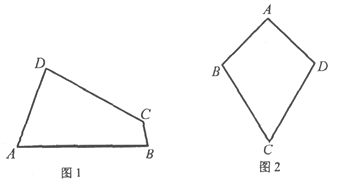
【题目】类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com