
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.
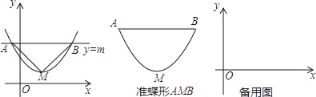
(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
【答案】(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,(2)2,4;(3)①y=
AB,(2)2,4;(3)①y=![]() x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
【解析】
(1)直接利用等腰直角三角形的性质分析得出答案;
(2)利用已知点为B(m,m),代入抛物线解析式进而得出m的值,即可得出AB的值;
(3)①根据题意得出抛物线必过(3,0),进而代入求出答案;
②根据y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,
AB,
如图1,∵△AMB是等腰直角三角形,且N为AB的中点,
∴MN⊥AB,MN=![]() AB,
AB,
故答案为:MN⊥AB,MN=![]() AB;
AB;

(2)∵抛物线y=![]() 对应的准蝶形必经过B(m,m),
对应的准蝶形必经过B(m,m),
∴m=![]() m2,
m2,
解得:m=2或m=0(不合题意舍去),
当m=2则,2=![]() x2,
x2,
解得:x=±2,
则AB=2+2=4;
故答案为:2,4;
(3)①由已知,抛物线对称轴为:y轴,
∵抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
∴抛物线必过(3,0),代入y=ax2﹣4a﹣![]() (a>0),
(a>0),
得,9a﹣4a﹣![]() =0,
=0,
解得:a=![]() ,
,
∴抛物线的解析式是:y=![]() x2﹣3;
x2﹣3;
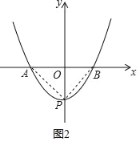
②由①知,如图2,y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
∴在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
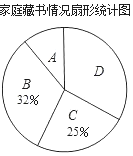
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商经销一种高档水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.1元,销售量将减少1千克
(1)现该商场保证每天盈利1500元,同时又要照顾顾客,那么每千克应涨价多少元?
(2)若该商场单纯从经济利益角度考虑,这种水果每千克涨价多少元,使该商场获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
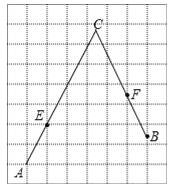
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
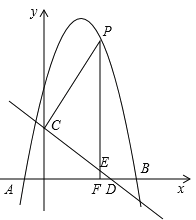
【题目】如图,抛物线![]() 与
与![]() 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线![]() 与y轴交于点
与y轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,是否存在点
的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com