
【题目】如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
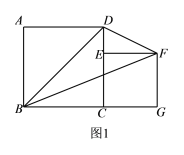
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .
(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想;
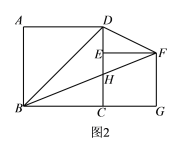
(3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长.
,求正方形CEFG的边长.
【答案】(1)18,18;(2)S△BDF=![]() S正方形ABCD,证明见解析;(3)4
S正方形ABCD,证明见解析;(3)4
【解析】
(1)根据三角形的面积公式求解;
(2)连接CF,通过证明BD∥CF,可得S△BDF=S△BDC=![]() S正方形ABCD;
S正方形ABCD;
(3)根据S△BDF= S△BDC可得S△BCH= S△DFH=![]() ,由三角形面积公式可求CH,DH的长,再由三角形面积公式求出EF的长即可.
,由三角形面积公式可求CH,DH的长,再由三角形面积公式求出EF的长即可.
(1)∵当点E与点D重合时,
∴CE=CD=6,
∵四边形ABCD,四边形CEFG是正方形,
∴DF=CE=AD=AB=6,
∴S△BDF=![]() ×DF×AB=18,
×DF×AB=18,
当点E为CD的中点时,如图,连接CF,
∵四边形ABCD和四边形CEFG均为正方形;
∴∠CBD=∠GCF=45°,
∴BD∥CF,
∴S△BDF=S△BDC=![]() S正方形ABCD=
S正方形ABCD=![]() ×6×6=18,
×6×6=18,
故答案为:18,18.
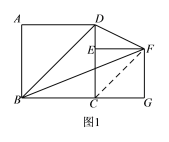
(2)S△BDF=![]() S正方形ABCD,
S正方形ABCD,
证明:连接CF.

∵四边形ABCD和四边形CEFG均为正方形;
∴∠CBD=∠GCF=45°,
∴BD∥CF,
∴S△BDF= S△BDC=![]() S正方形ABCD;
S正方形ABCD;
(3)由(2)知S△BDF= S△BDC,
∴S△BCH= S△DFH=![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴EF=4,
∴正方形CEFG的边长为4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证:(1)△ABE≌△AEF;(2) AD+BC=AB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
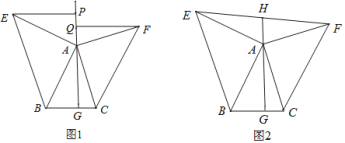
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
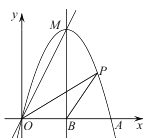
(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,![]() .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
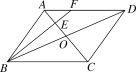
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
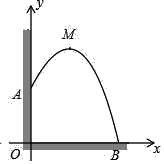
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与地面垂直).抛物线的最高点M离墙1m,离地面![]() m.
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式.
(2)求水的落地点B与点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com