



 一次函数y=
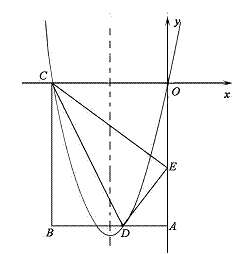
一次函数y= x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点 C的坐标;
C的坐标;
(2)设二次函数图像的 顶点为D.
顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.
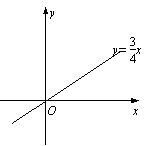
(1)y=ax2-4ax+c=a(x-2)2-4a+c.∴二次函数图像的对称轴为直线x=2.
当x=2时,y= x=
x=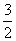 ,∴C(2,
,∴C(2,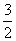 ).
).
(2)①∵点D与点C关于x轴对称,∴D(2,-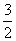 ,),∴CD=3.
,),∴CD=3.
设A(m, m) (m<2),由S△ACD=3,得
m) (m<2),由S△ACD=3,得 ×3×(2-m)=3,解得m=0,∴A(0,0).
×3×(2-m)=3,解得m=0,∴A(0,0).
由A(0,0)、 D(2,-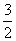 )得
)得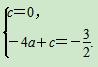 解得a=
解得a=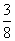 ,c=0.
,c=0.
∴y=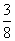 x2-
x2-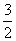 x.
x.
②设A(m, m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=
m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=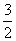 -
- m,
m,
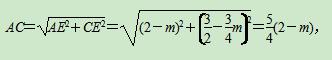 ∵CD=AC,∴CD=
∵CD=AC,∴CD= (2-m).
(2-m).
由S△ACD=10得 ×
× (2-m)2=10,解得m=-2或m=6(舍去),∴m=-2.
(2-m)2=10,解得m=-2或m=6(舍去),∴m=-2.
∴A(-2,-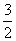 ),CD=5.
),CD=5.
若a>0,则点D在点C下方,∴D(2,-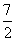 ),
),
由A(-2,-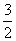 )、D(2,-
)、D(2,-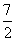 )得
)得
∴y=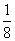 x2-
x2- x-3.
x-3.
若a<0,则点D在点C上方,∴D(2, ),
),
由A(-2,-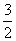 )、D(2,
)、D(2, )得
)得
∴y=- x2+2x+
x2+2x+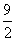 .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的解析式;
(3)一动点P 从点C 出发,沿CB 以每秒2 个单位长的速度向点B 运动,同时动点Q 从E 点出发,沿EC 以每秒1 个单位长的速度向点C 运动,当点P 到达点B 时,两点同时停止运动.设运动时间为t 秒,当t为何值时,DP=DQ;
(4) 若点N 在(2)中的抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E 为顶点的四边形是平行四边形?若存在,请求出M 点的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
为筹备班级毕业晚会,班长对全班同学爱吃哪几种水果作了民意调查.根据调查数据决定最终买什么水果应参照的统计量是( ).
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
| 分数段(分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x<90 | 16 | b% |
| 90≤x<100 | 4 |
|
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com