Question

如图1和图2，在20×20的等距网格（每格边长是1个单位）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位的速度先向下平移，当BC边与网的底部重合时，继续以同样的速度向右平移，当点C与点P重合时Rt△ABC停止移动.

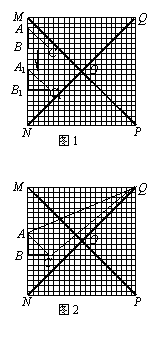设运动时间为x秒，△QAC的面积为y.

（1）如图1，当Rt△ABC向下平移到Rt△A₁B₁C₁的位置时，在

网格中画出Rt△A₁B₁C₁关于直线QN成轴对称的图形；

（2）如图2，在Rt△ABC向下平移的过程中，求出y与x的函数

关系式，并直接写出当x取何值时，y取得最大值和最小值？

最大值和最小值分别是多少？

（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，

y取得最大值和最小值？最大值和最小值分别是多少？

Answer 1

（1）画图略………………………………………………………………………………（2分）

（2）y＝2x＋40（0≤x≤16）……………………………………………………………（4分）

当x＝0时，y取得最小值，y_最小＝40.……………………………………………（5分）

当x＝16时，y取得最大值，y_最大＝72.……………………………………………（6分）

（3）y＝－2x＋104（16≤x≤32）………………………………………………………（8分）

当x＝16时，y取得最大值，y_最大＝72.……………………………………………（9分）

当x＝32时，y取得最小值，y_最小＝40.…………………………………………（10分）

【或用轴对称的思想解释，在△ABC自左向右平移的过程中，均对应着（2）中自上而下平移的某个位置，这两个三角形关于直线QN成轴对称，也能确定面积的最大、最小值】