
【题目】如图,在四边形ABCD中,BD为一条对角线,∠ABD=90°,AD∥BC, AD=2BC,E为AD的中点,连接BE.

(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,则AC的长为 .
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
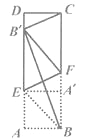
【题目】如图,将矩形纸片ABCD折叠,使点A与BC边上的点A′重合,折痕为BE,再沿过点E的直线折叠,使点B与AD边上的点 B重合,折痕为EF,连结![]() ,
,![]() .
.![]() ,则
,则![]() 的值为________
的值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解答问题:
数学大师的名题与方程
欧拉是18世纪瑞士著名的数学大师.他的一生都致力于数学各个领域的研究,并取得非凡的成就.在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题.他构思这些问题的初衷,正是为了强化方程解题的适用和便利.
请用适当的方法解答下面问题:
父亲死后,四个儿子按下述方式分了他的财产:老大拿了财产的一半少3000英镑:老二拿了财产的![]() 少1000英镑;老三拿了恰好是财产的
少1000英镑;老三拿了恰好是财产的![]() ;老四拿了财产的
;老四拿了财产的![]() 加上600英镑.问整个财产有多少?每个儿子各分了多少?
加上600英镑.问整个财产有多少?每个儿子各分了多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,
表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | |
压强增加值 Y(kpa) | 0 | 9.5 | 18 | 25.5 | 32 | 37.5 | 42 |
(1)根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);
(2)y与t之问是否存在函数关系?若是,请求出函数关系式;否则请说明理由;
(3)①在该模式下,压强P的最大值是多少?
②当t分别为,t1,t2(t1<t2)时,对应y的值分别为y1 ,y2 , 请比较![]() 与
与![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华根据学习函数的经验,对函数![]() 的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
| 4 | 5 |
|
|
| m | 2 | 1 | 0 | n | 2 | 3 |
|
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;

(3)观察图象,写出该函数的两条性质;
(4)进一步研究函数图象发现:
①方程![]() 有 个实数根;
有 个实数根;
②不等式![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过___________秒后边OC与边ON互相垂直.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() ,
,![]() 为原点.
为原点.
(1)试求![]() 和
和![]() 的值;
的值;
(2)点![]() 从
从![]() 点出发向右运动,经过3秒后点
点出发向右运动,经过3秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的3倍,求点
点距离的3倍,求点![]() 的运动速度?
的运动速度?
(3)点![]() 以一个单位每秒的速度从点
以一个单位每秒的速度从点![]() 向右运动,同时点
向右运动,同时点![]() 从点
从点![]() 出发以5个单位每秒的速度向左运动,点
出发以5个单位每秒的速度向左运动,点![]() 从点
从点![]() 出发,以20个单位每秒的速度向右运动.在运动过程中,
出发,以20个单位每秒的速度向右运动.在运动过程中,![]() 分别为
分别为![]() 的中点,问
的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com