
【题目】某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,
表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | |
压强增加值 Y(kpa) | 0 | 9.5 | 18 | 25.5 | 32 | 37.5 | 42 |
(1)根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);
(2)y与t之问是否存在函数关系?若是,请求出函数关系式;否则请说明理由;
(3)①在该模式下,压强P的最大值是多少?
②当t分别为,t1,t2(t1<t2)时,对应y的值分别为y1 ,y2 , 请比较![]() 与
与![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
【答案】(1)见解析;(2)![]() ;(3)①p=150,②
;(3)①p=150,②![]() >
>![]() 实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.
实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.
【解析】(1)根据表中提供的数据,在直角坐标系中,描出各个点即可;
(2)观察点的坐标特点,图像过(0,0),因此设y与t之间的函数关系式为:y=at2+bt,求出函数解析式,再验证其它的点是否满足此函数解析式,即可求解;
(3)①根据(2)中的函数解析式,求出顶点坐标,得出y的最大值,再根据y=p-100,可求出压强p的最大值;②先求出y1与t1的比值及y2与t2的比值,根据t1<t2即可求解.
(1)如图
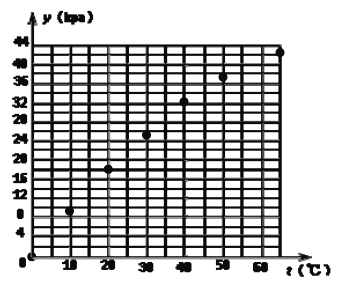
(2)∵图像经过(0,0)(10,9.5),(20,18),
∴设y与t之间的函数关系式为:y=at2+bt,
∴![]() ,
,
![]()
解之: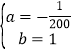 ,
,
∴y与t的函数关系为:![]() ,
,
经验证:其它的各个点都满足该函数解析式.
(3)解:①![]() ,
,
当t=100,y有最大值是50,
∵y=p-100=50,
∴p=150,
在该模式下,压强P的最大值是150;
②当t分别为:t1 ,t2(t1<t2)时,![]() ,
,![]() ,
,
∵t1<t2
∴![]() >
>![]()
实际意义是:从加热起到t1°C,平均每1°C增加的压强,要大于从加热起到t2°C时,平均每1°C增加的压强.


科目:初中数学 来源: 题型:
【题目】如图,半径为1的![]() 的圆心A在抛物线y=(x-3)2-1上,AB//x轴交
的圆心A在抛物线y=(x-3)2-1上,AB//x轴交 ![]() 于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )
于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )

A. y=(x-4)2-1 B. y=(x-3)2 C. y=(x-2)2-1 D. y=(x-3)2-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(x-3)(x-5)=m(m>0)有两个实数根![]() ,
,![]() (
( ![]() <
<![]() ),则下列选项正确的是( )
),则下列选项正确的是( )
A. 3<![]() <
<![]() <5 B. 3<
<5 B. 3<![]() <5<
<5<![]() C.
C. ![]() <2<
<2<![]() <5 D.
<5 D. ![]() <3且
<3且![]() >5
>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得![]() .
.
(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(6)班为从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评.其中,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表;另全班50位同学参与民主测评进行投票,结果如下图:
![]()
A | B | C | D | E | |
甲 | 89 | 91 | 92 | 94 | 93 |
乙 | 90 | 86 | 85 | 91 | 94 |

规定: 演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的平均分;
(2)民主测评统计图中a= ,b= ;
(3)求甲、乙两位选手的民主测评得分;
(4)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,∠ABD=90°,AD∥BC, AD=2BC,E为AD的中点,连接BE.

(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,则AC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,那么下列条件中不能判定四边形
,那么下列条件中不能判定四边形![]() 是菱形的为( )
是菱形的为( )
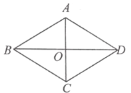
A. ∠OAB=∠OBAB. ∠OBA=∠OBCC. AD∥BCD. AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com