Question

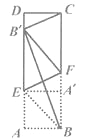
【题目】如图，将矩形纸片ABCD折叠，使点A与BC边上的点A′重合，折痕为BE，再沿过点E的直线折叠，使点B与AD边上的点 B重合，折痕为EF，连结,．，则的值为________

Answer 1

【答案】

【解析】根据矩形纸片ABCD折叠，使点A与BC边上的点 A ′ 重合，折痕为BE，可证得四边形ABA′ E是正方形，设AB=x，则BE=x，再根据再沿过点E的直线折叠，使点B与AD边上的点 B ′ 重合，折痕为EF，证得易证四边形B′EBF是菱形，求出B′E、A′F的长，然后证明△CB′D≌△EFA′，可证得DB′=A′F，根据AD=AE+B′E+B′D，可得出结果.

如图，设EF与BB交于点O

∵矩形纸片ABCD折叠，使点A与BC边上的点 A ′ 重合，折痕为BE

∴AB=AB,∠A=∠ABA′ ，∠EA′ B=90°

∴四边形ABA′ E是正方形，

设AB=x，则BE=x

∵再沿过点E的直线折叠，使点B与AD边上的点 B ′ 重合，折痕为EF

∴易证四边形B′EBF是菱形，

∴BF=BE=B′E=x，B′ B⊥EF，

∴∠BB′ F=∠FBB′ ,∠FOB=90°

∵∠DCB′ =∠BB′ F

∴∠DCB′ =∠FBB′

∵∠1+∠FEA′=90°，∠1+FBO=90°

∴∠FEA′=∠FBO=∠DCB′

在△CB′D和△EFA′中

∴△CB′D≌△EFA′（ASA）

∴DB′=A′F

∴A′F=BF-BA′=x-x

∴AD=AE+B′E+B′D=x+x+x-x=2x

∴

故答案为：2.