
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,过
,过![]() 作
作![]() ∥
∥![]() 交
交![]() 的延长线于
的延长线于![]() .若四边形
.若四边形![]() 的周长是
的周长是![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 的周长.
的周长.

【答案】30cm
【解析】
由三角形中位线定理推知ED∥FC,2DE=BC,然后结合已知条件“EF∥DC”,利用两组对边相互平行得到四边形DCFE为平行四边形,根据在直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC,即可得出四边形DCFE的周长=AB+BC,故BC=25AB,然后根据勾股定理即可求得.
解:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又 EF∥DC,
∴四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25AB)2+52,
解得,AB=13cm,∴BC=12cm,
∴![]() 的周长=13+12+5=30cm.
的周长=13+12+5=30cm.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠BAC=100°.
(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;
(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;
(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
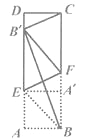
【题目】如图,将矩形纸片ABCD折叠,使点A与BC边上的点A′重合,折痕为BE,再沿过点E的直线折叠,使点B与AD边上的点 B重合,折痕为EF,连结![]() ,
,![]() .
.![]() ,则
,则![]() 的值为________
的值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解答问题:
数学大师的名题与方程
欧拉是18世纪瑞士著名的数学大师.他的一生都致力于数学各个领域的研究,并取得非凡的成就.在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题.他构思这些问题的初衷,正是为了强化方程解题的适用和便利.
请用适当的方法解答下面问题:
父亲死后,四个儿子按下述方式分了他的财产:老大拿了财产的一半少3000英镑:老二拿了财产的![]() 少1000英镑;老三拿了恰好是财产的
少1000英镑;老三拿了恰好是财产的![]() ;老四拿了财产的
;老四拿了财产的![]() 加上600英镑.问整个财产有多少?每个儿子各分了多少?
加上600英镑.问整个财产有多少?每个儿子各分了多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过___________秒后边OC与边ON互相垂直.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com