
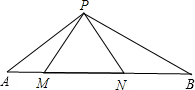
 如图,△PMN是等边三角形,∠APB=120°.
如图,△PMN是等边三角形,∠APB=120°.分析 (1)由△PMN是等边三角形,∠APB=120°,可得∠AMP=∠PNB=120°,继而证得∠APM=∠B,则可证得△APM∽△PBN,然后由相似三角形的对应边成比例,证得结论;
(2)由△APB是等腰三角形,可得∠A=∠B=30°,继而可得AM=PM=BN=PN,然后过点N作NH⊥PB于点H,即可求得AP=PB=$\sqrt{3}$NB,继而求得答案.
解答 (1)证明:∵△PMN是等边三角形,
∴∠PMN=∠PNM=60°,
∴∠AMP=∠PNB=120°,
∴∠A+∠APM=60°,
∵∠APB=120°,
∴∠A+∠B=60°,
∴∠APM=∠B,
∴△APM∽△PBN,
∴AM:PN=AP:PB,
∴AM•PB=PN•AP.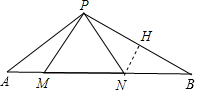
(2)∵△APB是等腰三角形,∠APB=120°,
∴∠A=∠B=30°,
∵△APM∽△PBN,
∴∠APM=∠A=∠BPN=∠B=30°,
∴AM=PM=BN=PN,
过点N作NH⊥PB于点H,
则BH=BN•cos30°=$\frac{\sqrt{3}}{2}$NB,BH=PH=$\frac{1}{2}$PB,
∴AP=PB=2BH=$\sqrt{3}$NB,
∴$\frac{AP}{NB}$=$\sqrt{3}$.
点评 此题考查了相似三角形的判定与性质、等边三角形的性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -2 | -4 | +12 | -10 | +16 | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知正方形OABC的顶点坐标分别为O(0,0),A(3,0),B(3,3),C(0,3).
如图,在平面直角坐标系中,已知正方形OABC的顶点坐标分别为O(0,0),A(3,0),B(3,3),C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com