
分析 欲判断是否可以构成直角三角形,只需验证两小边的平方和是否等于最长边的平方,即可得出答案.
解答 解:①62=36,82=64,102=100,362+642≠1002,不能构成直角三角形;
②($\frac{1}{5}$)2+($\frac{1}{4}$)2≠($\frac{1}{3}$)2,不能构成直角三角形;
③12+($\sqrt{2}$)2=($\sqrt{3}$)2,能构成直角三角形;
④82+152=172,能构成直角三角形;
⑤3002+4002=5002,能构成直角三角形.
故答案为:③④⑤.
点评 此题主要考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
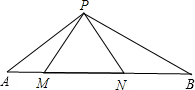 如图,△PMN是等边三角形,∠APB=120°.
如图,△PMN是等边三角形,∠APB=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC和∠ACB,求∠BDC的度数.
(1)如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC和∠ACB,求∠BDC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=-1 x2=-4 | B. | x1=1 x2=4 | C. | x1=-1 x2=4 | D. | x1=2 x2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
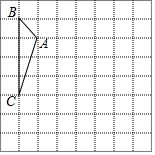 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com