练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，点E、F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（　　）
    A．AD∥BCB．DF∥BEC．∠D=∠BD．∠A=∠C

    分析 全等三角形的判定定理有SAS，ASA，AAS，SSS，根据以上定理逐个进行判断即可．

    解答 解：∠D=∠B，
    理由是：∵在△ADF和△CBE中
    $\left\{\begin{array}{l}{AD=BC}\\{∠D=∠B}\\{DF=BE}\end{array}\right.$
    ∴△ADF≌△CBE（SAS），
    即选项C正确；
    具备选项A、选项B，选项D的条件都不能推出两三角形全等，
    故选C．

    点评 本题考查了全等三角形的判定定理的应用，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．若-4a5b2m与3a2m+3bn+3的和仍一个是单项式，则m、n的值分别是（　　）
    A．1，-1B．1，2C．1，-2D．1，1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列关于x的方程中，一定是一元二次方程的为（　　）
    A．2x+3=0B．x2-2=（x+3）2C．${x^2}=\frac{1}{x}$D．x2-1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

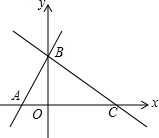    5．如图，一次函数y=（m-1）x+4的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB面积为4．
    （1）求m的值及点A的坐标．
    （2）过点B作直线BC与x轴的正半轴相交于点C，且OC=3OA，求直线BC的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．小张、小王和另两名同学一起去看电影《寻龙诀》，小张买到4张座位相连的电影票，座位号顺次为8排3、4、5、6座．现在小张和小王从中随机各抽取一张电影票，求小张和小王抽取的电影票正好是相邻座位的概率（请通过画树状图或列表法写出分析过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

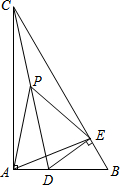    2．如图，Rt△ABC中，∠CAB=90°，∠ACB=30°，D是AB上一点（不与A、B重合），DE⊥BC于E，若P是CD的中点，请判断△PAE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

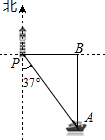    9．如图，一艘海轮位于灯塔P的南偏东37°方向，距离灯塔40 海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的正东方向上的B处．这时，B处与灯塔P的距离BP的长可以表示为（　　）
    A．40海里B．40tan37°海里C．40cos37°海里D．40sin37°海里

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知反比例函数$y=\frac{k-1}{x}$图象的两个分支分别位于第一、第三象限．
    （1）求k的取值范围；
    （2）取一个你认为符合条件的K值，写出反比例函数的表达式，并求出当x=-6时反比例函数y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列图形中，轴对称图形的个数为（　　）
    A．1个B．2 个C．3个D．4个

    查看答案和解析>>

    同步练习册答案