
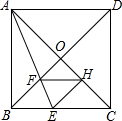
 如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )
如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)利用折叠的性质得出∠BAE=∠EAH=22.5°,进而得出∠DAF=67.5°,利用三角形内角和得出∠AFD=67.5°,证明AD=DF正确;
(2)利用角平分线的性质得出EB=EH,再利用三角形面积公式得出$\frac{{S}_{△ABE}}{S△ACE}$=$\frac{AB}{AC}$,正确;
(3)根据tan∠BAE=tan22.5°≈0.41,利用菱形得出FH=BE,进而得出$\frac{FH}{AD}$=$\sqrt{2}$-1,正确;
(4)我们根据折叠的性质就能得出BE=EH,BF=FH,只要再证出BE=BF就能得出BEHF是菱形,可用角的度数进行求解,得出∠BFA的度数,那么就能求出∠BFE的度数,在直角三角形ABE中,有了∠BAE的度数,就能求出∠AEB的度数,这样得出BE=BF后就能证出BEHF是菱形了.
解答 解:(1)∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴∠BAE=∠EAH=22.5°,
∴∠DAF=67.5°,
∴∠AFD=67.5°,
∴AD=DF,
故(1)正确;
(2)∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴△ABE≌△AEH,
∴BE=EH,
∴$\frac{{S}_{△ABE}}{S△ACE}$=$\frac{\frac{1}{2}AB•BE}{\frac{1}{2}AC•EH}=\frac{AB}{AC}$,
故(2)正确;
(3)∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴∠BAE=22.5°,
∴tan∠BAE=tan22.5°=$\sqrt{2}-1$,
(4)∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AB落在AC上,点B恰好与AC上的点H重合,
∴BE=EH,BF=FH,
又∵FH∥BC,
∴∠AEB=∠EFH,
又∵∠AEB=∠AFH,
∴∠AFH=∠EFH,
∴BE=EH=FB=BH,
∴四边形BEHF是菱形,
故(4)正确;
∴tan∠BAE=$\frac{BE}{AB}=\frac{FH}{AD}$,
故(3)正确.
故选D.
点评 主要考查了正方形的性质,菱形的判定,相似三角形的判定和性质等知识点,根据折叠的性质的角和边相等是解题的关键.折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查我区奶制品中蛋白质含量是否达到国家标准 | |
| B. | 调查我区6月1日这天嘉陵江水中氨氮含量是否超标 | |
| C. | 调查我校初三某班全体学生的视力状况 | |
| D. | 调查我区市民对消防安全知识的知晓情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com