
如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值;
(2)求抛物线E2所表示的二次函数的表达式;
(2)在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.


【考点】二次函数综合题.
【分析】(1)将A(1,m)代入y=x2,求得m的值即可;
(2)设抛物线E2的函数表达式为y=ax2(a≠0),将点B(2,2)代入抛物线的解析式求得a的值即可;
(3)当∠BB′Q=90°时,将x=2代入y=x2,可求得点Q的纵坐标,当∠BQB′=90°时,设点Q2的坐标为(t,t2),依据两点间的距离公式和勾股定理的逆定理列出关于t的方程求解即可.
【解答】解:(1)∵抛物线E1经过点A(1,m)
∴m=12=1
(2)∵抛物线E2的顶点在原点,可设它对应的函数表达式为y=ax2(a≠0)
又∵点B(2,2)在抛物线E2上
∴2=a×22,解得:a=

∴抛物线E2所对应的二次函数表达式为y=
 x2
x2
(3)如图所示:
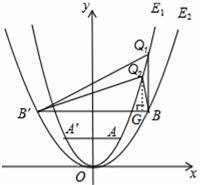

①当点B为直角顶点时,过B作Q1B⊥BB′交抛物线E1于Q,则点Q1与B的横坐标相等且为2,将x=2代入y=x2得y=4,
∴点Q1的坐标为(2,4).
②当点Q2为直角顶点时,则有Q2B′2+Q2B2=B′B2,过点Q2作GQ2⊥BB′于G,设点Q2的坐标为(t,t2)(t>0),则有(t+2)2+(t2﹣2)2+(2﹣t)2+(t2﹣2)2=4,
整理得:t4﹣3t2=0,
∵t>0,
∴t2﹣3=0,解得t1=
 ,t2=﹣
,t2=﹣
 (舍去),
(舍去),
∴点Q的坐标为(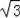
 ,3),
,3),
综上所述,存在符合条件的点Q坐标为(2,4)与(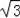
 ,3).
,3).
【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数图象上点的坐标与函数解析式的关系、待定系数法求二次函数的解析式、勾股定理的逆定理的应用、两点间的距离公式,依据勾股定理的逆定理和两点间的距离公式列出关于t的方程是解题的关键.


科目:初中数学 来源: 题型:
在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 5 | 10 | 5 | 15 | 10 |
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
A.30,35 B.50,35 C.50,50 D.15,50
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)


查看答案和解析>>
科目:初中数学 来源: 题型:
九年级某班40位同学的年龄如下表所示:
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 3 | 16 | 19 | 2 |
则该班40名同学年龄的众数和中位数分别是( )
A.19,15 B.15,14.5 C.19,14.5 D.15,15
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数
 图象上一点.将△AOB绕B点旋转至△A′O′B处.
图象上一点.将△AOB绕B点旋转至△A′O′B处.
(1)求m的值;
(2)若O′落在OC上,连接AA′交OC与D点.①求证:四边形ACA′O′为平行四边形; ②求CD的长度;
(3)直接写出当AO′最短和最长时A′点的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com